Машиностроение \ Теория механизмов и машин

Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 9

момент инерции кулисы = 0,25 кг× м×с2;

сила сопротивления резанию в данном положении механизма                     Р = 1500 Н.

Сначала производим построение планов скоростей (рис. 20,б) и ускорений (рис. 20,в) механизма при известной угловой скорости кривошипа

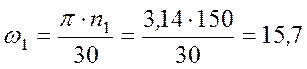 с-1.

Из плана ускорений определяем необходимые ускорения:

 м/с-2,

 м/с-2,

Силы инерции звеньев равны:

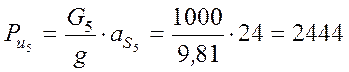 Н.

Эту силу прикладываем к точке S5

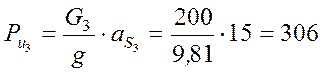 Н.

Так как кулиса вращается вокруг точки С, то сила инерции  кулисы будет приложена к центру качения звена (точке K3), положение которой на звене определяется с помощью формулы (5),

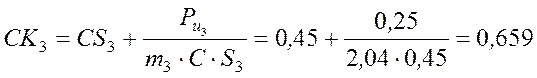 м.

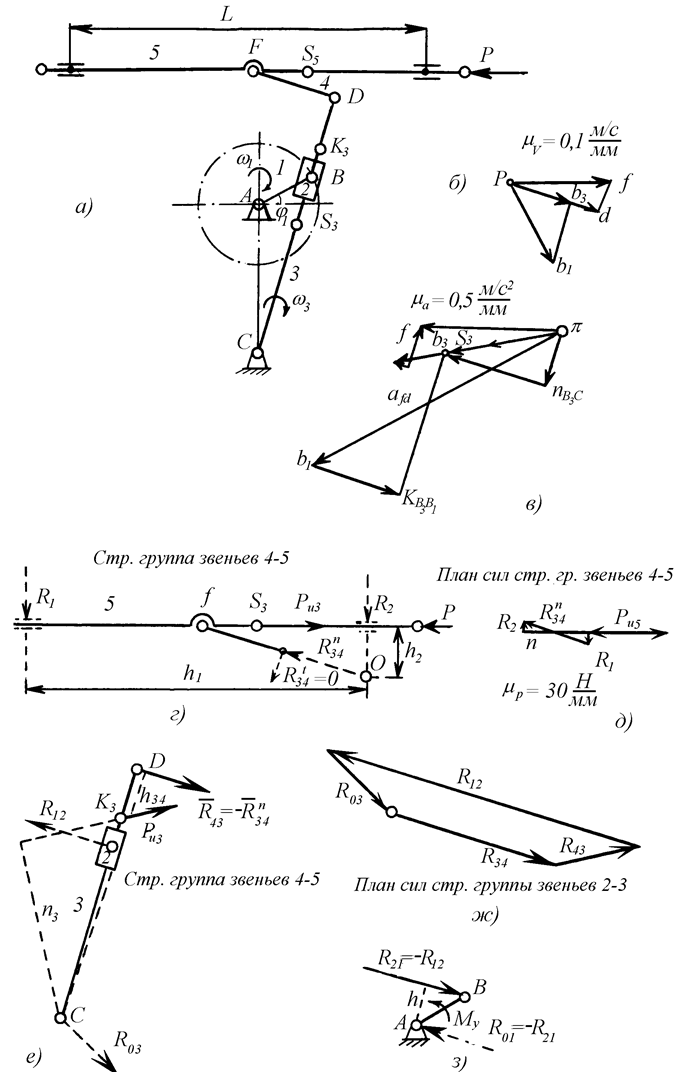
Рис. 20

Вектор  будет направлен в сторону, обратную направлению вектора pS3 на плане ускорений (рис. 20,в). Переходя к определению реакций в кинематических парах механизма, разложим его на структурные группы, вычертив их отдельно и приложив к ним все внешние силы.

Действие отброшенных частей заменяем реакциями`, , , , , ` и для структурной группы звеньев 4-5 (рис. 20,г) составляем уравнение равновесия ` +  + +  +  = 0. В этом уравнении реакция отсутствует, так как она равна нулю, что легко установить, рассмотрев уравнение моментов сил приложенных к звену 4 относительно точки F.

Из трех неизвестных векторов, входящих в уравнение, -,  и - один вектор необходимо определить с помощью уравнения моментов. Напишем уравнение моментов относительно точки О (см. рис. 20,г)

,

откуда

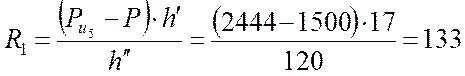 Н.

Остальные неизвестные силы определяем построением плана сил. Из полюса П (рис. 20,д) откладываем силу  в масштабеmn = 30 Н/мм, затем последовательно силы P, R1. Чтобы получить замкнутый многоугольник, через полюс П проведем направление силы R2. Точка пересечения этих направлений определяет длины неизвестных векторов  и R2. Умножая полученные отрезки на масштаб плана, получим:

 Н.

 Н.

Сила реакции во внутреннем шарнире будет равна силе реакции .

 Н.

Переходя к структурной группе звеньев 2-3 (рис. 20,е), напишем ее уравнение равновесия

.

Из уравнения моментов сил относительно точки С находим величину реакции .

,

откуда

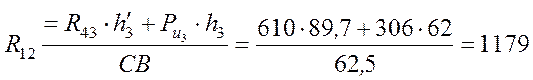 Н.

Из плана сил можно найти вектор

.

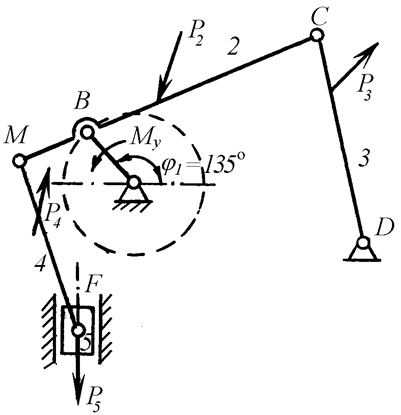
Рис. 21

Он будет замыкающим вектором четырехугольника, в котором стороны`, ,  известны. Построение этого плана показано на рис. 20,ж. Величина этой реакции будет равна

 Н.

Переходя к расчету ведущего звена (рис 20,з), определяем уравновешивающий момент по формуле

 Н×м.

Реакция R01 в шарнире А совместно с реакцией R21 будет образовывать пару сил, момент которой уравновешивается с моментом Му. Следовательно,

 Н.

Для усвоения методики силового расчета предлагается произвести определение сил реакций в общем виде для механизма, приведенного на            рис. 21, считая известными внешние силы , ,, и размеры звеньев механизма.

8.  ОПРЕДЕЛЕНИЕ  УРАВНОВЕШИВАЮЩЕГО  МОМЕНТА

С  ПОМОЩЬЮ  РЫЧАГА  ЖУКОВСКОГО

Силовой расчет механизма обычно заканчивается, как мы видим, определением уравновешивающего момента на ведущем звене механизма. На практике иногда требуется определить уравновешивающий момент, не определяя реакций в кинематических парах, нахождение которых требует длительных расчетов. Такая задача решается, например, в том случае, когда требуются по заданной силе полезных сопротивлений определить необходимую движущую силу на ведущем звене машины или определить силу полезного сопротивления, которую может преодолевать механизм при заданной движущей силе. Для решения данной задачи удобно использовать способ      Н. Е. Жуковского, впервые преложившего этот метод силового расчета механизмов. Способ Жуковского основан на применении к механизмам принципа возможных перемещений. Принцип можно сформулировать следующим образом: если под действием внешних сил , , , … , механическая система находится в равновесии и если системе дать возможное для данного ее положения перемещение, то сумма элементарных работ этих сил на любом возможном перемещении равна нулю.

Если система находится в движении, то, согласно принципу Даламбера, в число внешних сил должны входить также и силы инерции. В механизме действительные перемещения входят в число возможных перемещений. Поэтому математически принцип может быть выражен уравнением

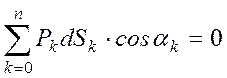,                                         (6)

Скачать файл