Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 10

где ds_k-действительное перемещение точки приложения силы P_k; a_k- угол между направлением перемещения ds_k и направлением силы P_k.

Разделив каждый член уравнения (6) на время dt, в течение которого совершается перемещение, получим

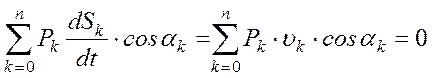,                           (7)

где u_k - скорость точки приложения силы P_k.

Выражение  - мощность, развиваемая силой P_k в данный момент. Теперь рассмотрим на рис. 22,а звено ВС механизма, к которому приложена сила P_kв точке k и для которого известны скорости точек звена u_k и u_с. В любом масштабе m_u.построим план скоростей звена (рис. 22,б).

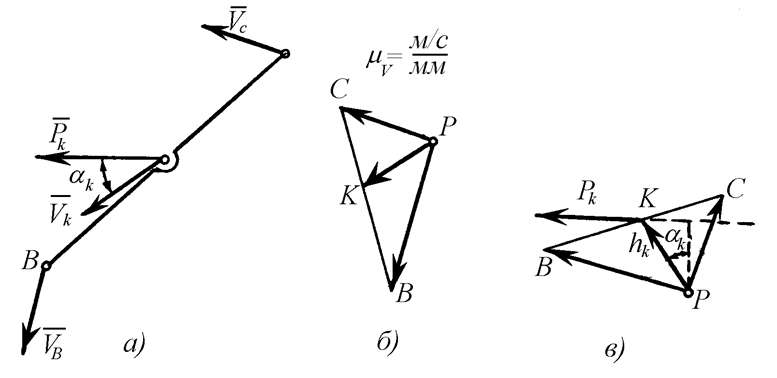
Рис. 22

Далее, повернем этот план на 90° в любую сторону и силу P_k перенесем из точки К звена ВС в соответствующую точку kповернутого плана скоростей (рис.22,в). Из полюса повернутого плана скоростей опустим перпендикуляр на линию действия силы P_k, получим отрезок h_k как плечо силы P_kотносительно полюса плана. Из условия перпендикулярности сторон kpd на плане будет равен углу . Так как из плана

.

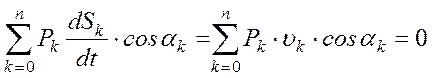Теперь напишем выражение момента силы P_k относительно полюса повернутого плана скоростей

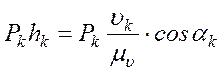.                                          (8)

Сравнивая полученное выражение момента (8) с уравнением (7) видим, что уравнение (7) можно написать в следующем виде:

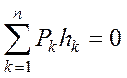                                                 (9)

Так как равенство (8) справедливо для всех сил P_k, приложенных к звеньям механизма, то общий для всех слагаемых множитель m_u отбрасывается. Полученный результат можно сформулировать так: если на механизм действует система сил, под действием которой он находится в равновесии, то повернутый план скоростей, рассматриваемый как жесткий рычаг с опорой в полюсе; под действием тех же сил, перенесенных в соответствующие точки плана, также находится в равновесии.

Уравнение (9) и является условием равновесия этого рычага. Этот вывод называется теоремой Жуковского о жестком рычаге. Если к звену механизма приложен момент, то его можно всегда заменить парой сил, приложенных в любых выбранных точках на этом звене.

Масштаб m_u плана скоростей может выбираться любым, так как в уравнение (9) он не входит. Поэтому практически удобно скорость одной из точек на плане изобразить отрезком произвольной длины, а затем графически определить остальные отрезки плана.

С помощью уравнения (9) можно определить величину силы, действующей на любое звено механизма, если известна точка приложения и линия действия этой силы.

Применяя теорему Жуковского, можно пользоваться также и неповернутым планом скоростей, но в этом случае при переносе сил на план скоростей их следует повернуть на угол 90° в одном и том же направлении. С помощью теоремы Жуковского можно также определить уравновешивающий момент М_у на ведущем звене механизма без определения реакций во всех кинематических парах механизма. Для этого уравновешивающий момент М можно представить в виде пары сил  и -. Одна из них приложена к оси вращения кривошипа А (рис. 23,а), а другая - в любой другой точке кривошипа, например М. Сила , приложенная к точке М, называется уравновешивающей силой. Наиболее удобно за вторую точку приложения силы пары брать шарнир В, а направление силы выбирать перпендикулярно кривошипу АВ (рис. 23,б). Тогда уравновешивающий момент M_yсвязан с уравновешивающей силой формулой

.                                           (10)

Рис. 23

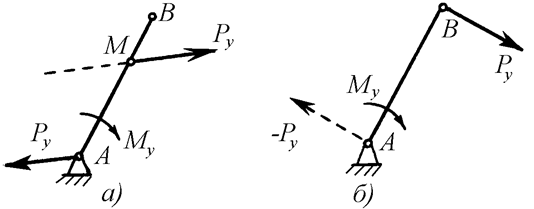
По теореме Жуковского определяютP_y, а по формуле (10)-М_у.

Проиллюстрируем определение уравновешивающего момента на примере механизма, изображенного на рис. 24. На рис. 24,а показан план скоростей этого механизма, в соответствующие точки которого перенесены силы, повернутые на 90° по направлению движения часовой стрелки.

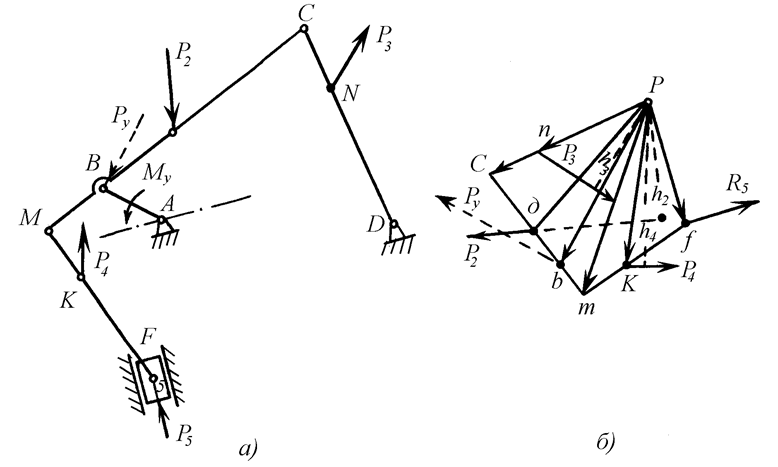
Рис. 24

Уравнение (9) для этого случая примет вид

,

Длины отрезков pf,h₄, h₃, h₂, рb берутся непосредственно с плана скоростей. Умножая полученную уравновешивающую силу Р_у на длину звена l_AB, получаем уравновешивающий момент M_y на ведущем звене механизма. С помощью теоремы Жуковского можно также проводить проверку правильности силового расчета механизма, так как моменты, полученные по теореме Жуковского и с помощью силового расчета механизма, должны совпадать.