Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 4

3вено совершает вращение вокруг оси, не проходящей через центр тяжести звена

Пусть звено вращается вокруг оси О (рис. 14), которая не проходит через центр тяжести звена S.

Силы инерции проводятся к одной силе Р_и, приложенной к точке S, и паре с моментом М_и. Чтобы заменить их одной равнодействующей, найдем плечо пары

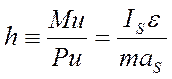                                         (4)

и отложим его от точки S так, чтобы равнодействующая сила Р_и вращала тело против направления e. Силы, приложенные к точке S взаимно уничтожаются, а равнодействующая Р_и пересечет направление OS в точке К.

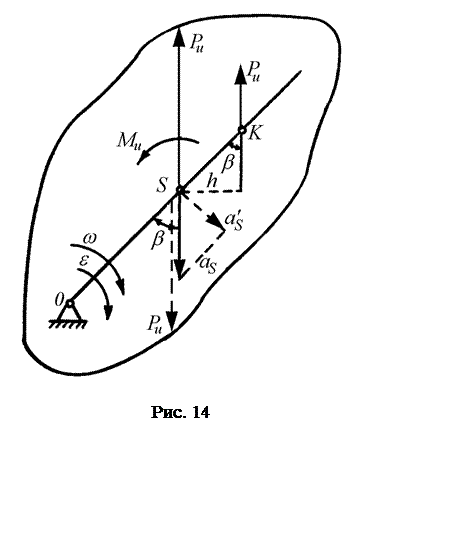Обозначая угол между ускорением а_S и радиусом OS через b, видим, что

.

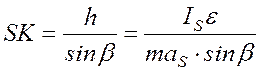С другой стороны, точка S вращается по кругу и ее касательное ускорение будет

,

но касательное ускорение определяется по формуле

,

следовательно,

.

Отсюда

.

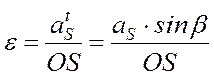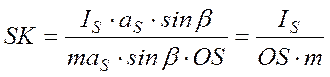Таким образом, точка приложения равнодействующей сил инерции К отстоит от центра вращения звена О на расстоянии

.

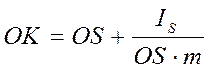Эта точка в механике называется центром качания звена.

Следовательно, чтобы учесть действие сил инерции в этом случае, достаточно найти по формуле (5) положение центра качания звена К и приложить к нему силу инерции Р_и, определяемую по формуле (1). Если звено вращается с постоянной угловой скоростью e = 0, то М_и = 0, b = 0 и равнодействующая сил инерции Р_и будет проходить по линии OS и направлена от центра вращения.

Звено вращается вокруг оси, проходящей через центр тяжести

Пусть звено вращается вокруг оси, проходящей через его центр тяжести S (рис. 15).

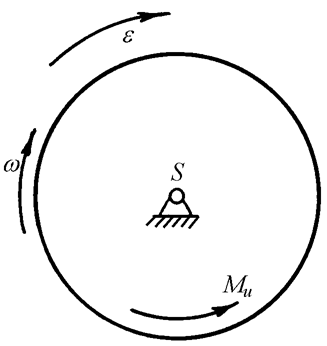
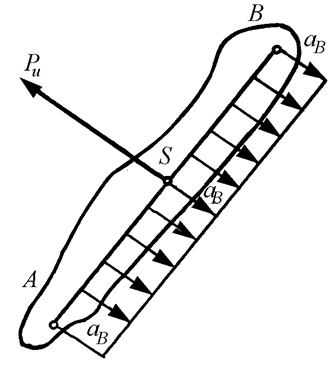
Рис. 15                                                Рис. 16

В этом случае, a_s = 0 и, следовательно, Р_и = 0. Остается пара с моментом 

М_и = -I_S ×e.

Если тело вращается с постоянной угловой скоростью, то e = 0 и результирующая сила инерции будет отсутствовать, т. е.

Р_и = 0;         М_и = 0.

Поступательное движение звена

При поступательном движении все точки тела описывают одинаковые траектории и имеют в каждый данный момент одинаковые скорости и ускорения (рис. 16). Следовательно, для этого случая и силы инерции приводятся лишь к одной равнодействующей , которая приложена к центру тяжести S звена. При равномерном и прямолинейном поступательном движении звена результирующая сила инерции будет равна нулю Р_и = 0, т. к. a_S = 0.

Кроме рассмотренного способа учета сил инерции с помощью определения равнодействующих сил инерции, применяется способ замены масс звеньев сосредоточенными массами, который также применяется в теории механизмов и описан в учебниках по ТММ. Примеры определения сил инерции звеньев механизмов приведены ниже в силовом расчете плоских механизмов.

5.  Реакции  в  кинематических  парах

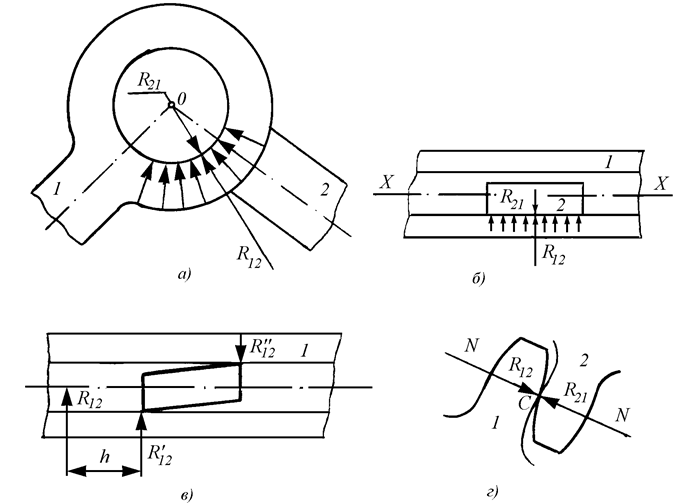
Реакциями в кинематических парах называются силы взаимодействия звеньев, образующих кинематическую пару. Эти силы при отсутствии трения всегда направлены по нормали к поверхности их касания. Поэтому, например, для вращательной пары (рис. 17,а) каждая элементарная сила взаимодействия будет направлена по радиусу и, следовательно, проходит через центры О вращательной пары. Равнодействующая всех элементарных сил также проходит через центр О. Условимся обозначать через R₂₁ силу действия звена 2 на звено 1, а через R₂₁ силу действия звена 1 на звено 2. Тогда, очевидно

R₁₂ = - R₂₁.

Для поступательной кинематической пары (рис. 17,б) все элементарные силы взаимодействия будут направлены перпендикулярно к направляющей х-х, следовательно, и результирующие реакции R₁₂ и R₂₁ также перпендикулярны направлению х-х. Однако линия действия результирующей реакции в зависимости от закона распределения элементарных сил может пройти как внутри поверхности соприкосновения звеньев (рис. 17,б) так и вне ее (рис. 17,в). В последнем случае будет перекос ползуна в направляющих и давления будут на нижней и верхней части направляющей. При этом силы  и  в общем случае не равны между собой. Их результирующаяR₁₂ может быть представлена одной силой, смещенной на расстояние h влево от края ползуна.