Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 7

Соединяя точку b плана с концом вектора , получим вектор  - реакцию в шарнире Е - как геометрическую сумму векторов  и . Чтобы определить реакцию в промежуточном шарнире F, достаточно воспользоваться тем же планом. Так как каждое звено структурной группы находится в равновесии, то многоугольник сил, действующих на каждое отдельное звено, также должен быть замкнутым. Рассмотрим звено 5 - ползун. На него действуют три силы: , и сила  или реакция со стороны звена 4. Две из этих сил уже построены на плане, следовательно, соединяя начало вектора  и конец вектора `, получим искомую силу `, которая в плане показана пунктиром. Таким образом, определены все реакции в структурной группе звеньев 4-5.

Переходим к следующей структурной группе звеньев 2-3, т. е. к решению уравнения (Б).

В этом уравнении четыре неизвестных по величине вектора, два из которых нужно определить из уравнений моментов сил, приложенных к каждому звену группы, относительно точки С. Получим два уравнения моментов:

,

.

Отсюда имеем

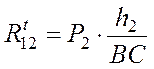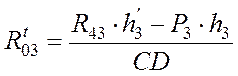 Н,                     Н.

Неизвестные векторы  и  определяются построением плана сил. Для этого из полюса П₁ плана строим вектор  (рис. 18,е) в масштабе μ_p Н/мм. Из конца  строим вектор , затем последовательно векторы ,,, а из конца последнего проводим направление вектора . Чтобы получить замкнутый многоугольник, из полюса П₁ проводим направление вектора . Пересечение этих двух направлений в точке b дает решение задачи.

Соединяя начало вектора ` и конец вектора , постучим полную реакцию в шарнире B, т. е. . Соединяя начало вектора  и конец вектора , получим полную реакцию в шарнире D, т. е. `.

Чтобы найти реакцию в промежуточном шарнире С, нужно построить замкнутый многоугольник сил, действующих на одно звено группы, например звено 2.

На него действуют силы , , и сила `реакции звена 3 на звено 2, которая неизвестна. Первые три силы уже имеются на плане сил, поэтому, соединяя конец вектора  с началом вектора  получим замыкающую, которая и дает вектор `, отмеченный на рис. 18,е пунктиром. Таким образом, все реакции в структурной группе звеньев 2-3 определены.

Переходим к исходному механизму. На кривошип действуют силы `, ` и уравновешивающий момент M_y, под действием которых он будет в равновесии. Векторное уравнение равновесия имеет вид

.

Отсюда следует, что силы `, и` представляют пару сил с плечом h.

Уравновешивающий момент M_y по величине будет равен и противоположно направлен моменту пары сил ` и` следовательно,

.

Таким образом, можно наметить следующую последовательность силового расчета многозвенного механизма:

1. Схема данного механизма разлагается на структурные группы, которые вычерчиваются на чертеже отдельно в масштабе со всеми внешними силами, действующими на их звенья.

2. В каждой структурной группе воздействие отброшенных частей механизма заменяют силами реакций, которые в шарнирах целесообразно представлять в виде двух составляющих, направленных вдоль звена и перпендикулярно направлению стержня звена.

3. Для каждой структурной группы записываются векторные уравнения, в которых часть неизвестных векторов, обычно направленных перпендикулярно стержню звена, определяется по величине из простейших уравнений равновесия , составленных для одного звена, а остальные неизвестные реакции определяются построением планов сил.

4. Построение планов сил начинают с последней, в порядке присоединения, структурной группы и заканчивают расчетом ведущего звена. При этом необходимо отметить следующее:

а) если внешние силы, например силы инерции, до силового расчета неизвестны, то их надо предварительно определить;

б) реакция R₀₁, на валу кривошипа равна по величине реакции R₂₁ в том случае, когда к валу приложен уравновешивающий моментM_y.

А последний будет в том случае, когда вал машины соединяется с валом двигателя муфтой, способной передавать лишь крутящий момент. В случае, когда соединение валов производится не муфтой, я посредством, например, зубчатой или ременной передачи, величина R₀₁ будет определяться иначе. Такой случай будет рассмотрен в следующих примерах.

7.  Примеры  расчета

Пример 1