Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 8

Определить реакции в кинематических парах механизма поршневого компрессора, схема которого приведена на рис. 19,а, при следующих данных:

угол поворота кривошипа j₁ = -30°;

число оборотов кривошипа n₁ = 160 об/мин;

длины звеньев, l_AB = 0,2 м, l_BC  = 0,8 м, ВS₂ = 0,2 м, где S₂- центр тяжести шатуна;

радиусы зубчатых колес r₁ = 0,45 м, r₂ =0,15 м;

вес ползуна G₃ = 40 Н;

вес шатуна G₂ =120 Н;

момент инерции шатуна относительно оси, проходящей через центр его тяжести, = 0,06 кг×м×с²;

сила давления воздуха на поршень в данном положении механизма           Р = 750 Н.

Прежде чем начать определение реакции в кинематических парах, необходимо определить силы инерции ползуна и шатуна. Для этого строим планы скоростей и ускорении механизма при

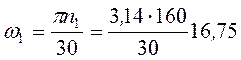 с^-1.

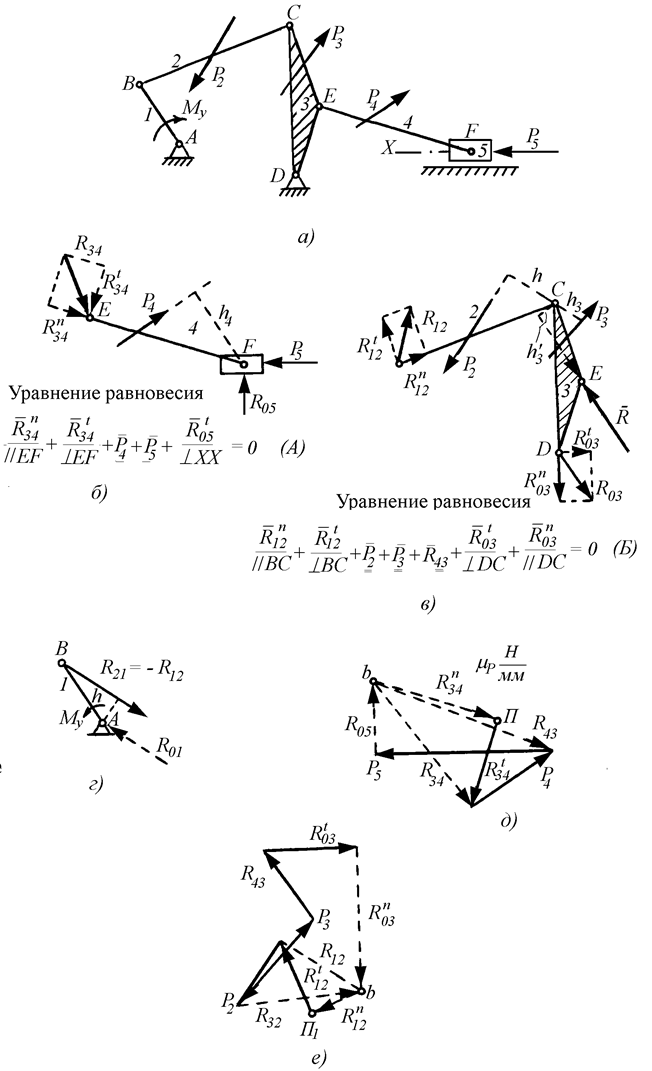
Рис. 19

Эти планы построены на рис. 19,б и 19,в, согласно которым найдено, что

 м/с^-2;

 м/с^-2;

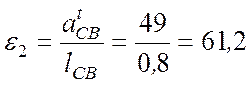 м/с^-2;

 с^-2.

Силы инерции звеньев 2 и 3 будут равны:

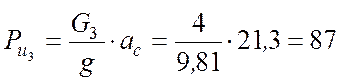 Н.

Плечо h силы  относительно центра тяжести шатуна, согласно формуле (4), равно

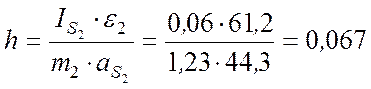 м.

Отложив плечо h в ту сторону от S₂, чтобы сила ,направленная в сторону, обратную вектору и вращая звено 2 против направления e, получим точку Т приложения этой силы. Силу  прикладываем к ползуну 3; она направлена вверх, т. е. против направления вектора ускорения a_c.

Определив таким образом все внешние силы, действующие на механизм, переходим к определению реакций в кинематических парах.

Для этого структурную группу звеньев 2-3 со всеми внешними силами вычертим отдельно (рис 19,г)

Здесь силы , и G₃ заменены одной силой

 кг.

Действие отброшенных частей заменяем реакциями , ,  и составляем векторное уравнение равновесия структурной группы. Имеем

.

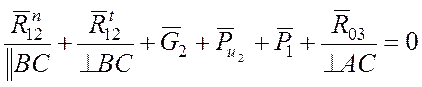Силу  по величине определяем из уравнения моментов всех сил, приложенных к шатуну, относительно шарнира С. Имеем

,

откуда

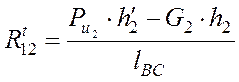 Н.

Измеряя отрезки , , по чертежу, получим:

 мм,  мм,  мм,

откуда

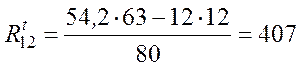 Н.

Для определения реакции и  строим план сил (рис. 19,д). Из полюса П плана последовательно откладываем известные векторы , , ,   в масштабе m_0. Из конца вектора  проводим направление вектора `, а из полюса П - направление вектора . Пересечение этих направлений дает точку В, которая определяет длины искомых векторов (на чертеже показаны пунктиром). Величины этих векторов будут равны:

 Н,  Н.

Полная реакция в шарнире В определяется по формуле

.

Из плана сил имеем

 Н.

Переходим к силовому расчету кривошипа, составляющего одно целое с зубчатым колесом (рис. 19,е).

К кривошипу в точке В приложена реакция  (действие шатуна на кривошип), которая по величине равна реакций  найденной по плану сил (см. рис. 19,д), и направлена в обратную сторону. Кроме того, к зубчатому колесу приложена сила давления Р_n на зубец со стороны другого колеса. Эта сила направлена по линии зацепления, наклоненной под углом 20° к общей касательной начальных окружностей зубчатых колес.

Величина этой силы определяется из уравнения моментов сил относительно точки А

.

По чертежу имеем значения  = 95 мм,= 21,2 мм. Отсюда

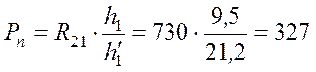 Н.

К ведущему звену также приложена реакция  в шарнире А. Совместно с известными силами P_n и R₂₁ она образует замкнутый треугольник сил, изображенный в масштабе m_Р= 10 Н/мм на рис. 19,ж, из которого и определяется по величине и направлению. В данном случае получим R₀₁ = 1044 Н.

Рассматривая равновесие другого зубчатого колеса (см. рис. 19,е), определяем уравновешивающий момент, приложенный со стороны двигателя. При h₀ = 0,14 м имеем:

M_y = Р_п ×h₀ = 327 × 0,14 = 45,78 Н×м.

Реакция на валу О определится как сила пары R₀ и -P_n, которая уравновешивает момент M_дв. Следовательно,

R₀ = P_n.

Направление этой реакции показано на рис. 19,е.

Пример2

Определить реакции в кинематических парах кулисного механизма станка от силы Р и сил инерции звеньев 5 и 3. Схема механизма приведена на рис. 20,а.

Дано: угол поворота кривошипа j₁ =30°, n₁ = 150 об/мин - число оборотов кривошипа АВ;

длины звеньев: l_AB = 0,2 м, l_CD  =0,9 .м, l_AC  = 0,5 м, l_DF=0,3 м;

расстояние между опорами ползуна L = 1,2 м,

центр тяжести кулисы взять посредине звена CD;

вес звеньев G₃= 200 Н,G₅= 1000 Н взять только при определении сил инерции звеньев. Весами звеньев G₁, G₂, G₄ в виду их малости можно пренебречь;