Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 3

В качестве примера на      рис. 11 показана характеристика центробежного насоса. Подробно вопросы о механических характеристиках машин освещаются в специальной литературе при решении вопросов подбора двигателей к рабочим машинам.

4.  Определение  сил  инерции  звеньев 

в  плоских  механизмах

При сложном плоском движении материальные точки звена имеют различные ускорения, следовательно, к каждой материальной точке звена может быть  отнесена  элементарная  сила  инерции  dP_i =-a_i×dm. Таким образом, получается система элементарных сил инерции (рис. 12) , которая, как известно из механики может быть сведена к одной результирующей силе инерции, приложенной к центру масс звена S, и одной результирующей паре сил.

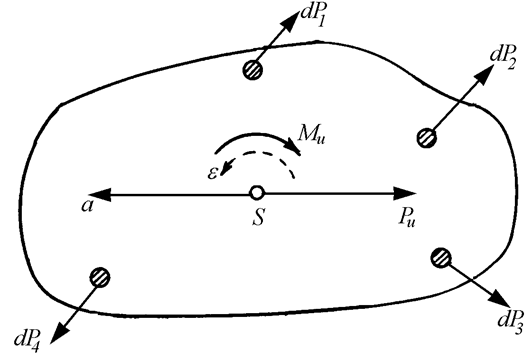
Рис. 12

Величина результирующей силы инерции  определяется по формуле

P_и = -m×a_s,                                             (1)

где m - масса всего звена; а_s - ускорение центра масс звена или его центра тяжести. Знак минус показывает, что сила инерции  направлена противоположно ускорению а_s. Момент пары сил инерции определяется по формуле

М_и= -I_S ×e ,                                               (2)

где e  - угловое ускорение звена; I_s - момент инерции звена относительно оси, перпендикулярной плоскости движения и проходящей через центр тяжести. Знак минус показывает, что момент М направлен противоположно угловому ускорению. Величина момента инерции определяется по формуле

,                                             (3)

где r - расстояние от элементарной массы до оси dm, проходящей через центр тяжести S, а интегрирование ведется по объему звена.

Для тел простой геометрической формы и постоянной плотности I_s может быть вычислен аналитически.

Например:

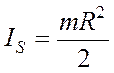 - для диска радиуса R;

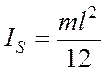 - для тонкого стержня длины l;

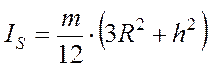 - для цилиндра радиуса R и высотой h и т. д. Здесь m – масса детали.

Тела сложной формы разбивают на ряд простых, заменяя интеграл (3) соответствующий суммой.

В ряде случаев достаточно точное определение моментов инерции тел сложных форм может дать опытное их определение, но для этого необходимо иметь в натуре само звено и соответствующую установку для опыта.

Замена всех сил инерции одной силой и одной парой применяется для решения задачи по определению реакций в кинематических парах механизмов. Однако при расчетах звеньев на прочность такой прием не всегда пригоден и инерционная нагрузка часто должна рассматриваться как определенная.

Из формул (1) и (2) видно, что для определения результирующих инерционных нагрузок Р_и и М_и необходимо знать ускорение центра тяжести звена а и угловое ускорение звена e, которые могут быть получены из кинематического расчета механизма.

Иногда бывает удобным результирующую, силу Р_и и результирующую пару с моментом М_и заменить одной равнодействующей Р_и, которая будет приложена уже не к центру тяжести S звена.

Рассмотрим этот прием в ряде частных случаев движения звена.

Звено совершает сложное движение

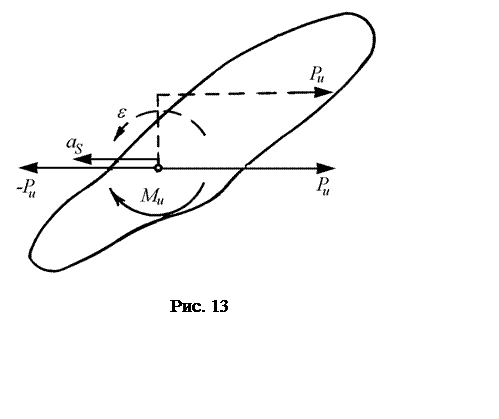Пусть звено (рис. 13) какого- либо механизма совершает сложное плоское движение, имея ускорение центра тяжести а_s и угловое ускорение e. В этом случае силы инерции проводятся к результирующей силе Р_и, приложенной к центру тяжести S звена и к паре с моментом М_и, вычисляемым по формулам (1) и (2). Вектор силы Р_и направлен а сторону, противополо-      жную а_s.

Чтобы заменить силу и момент одной равнодействующей силой Р_и представим пару сил инерции в виде двух противоположных сил Р_и и -Р_и. Силу -Р_и, приложим к точке        S, а Р_и - на расстоянии                   h = М_и/Р_и, отложенном так, чтобы эта пара сил имела момент, по величине и направлению равный М_и. Тогда силы Р_и и -Р_и, приложенные в точке S, взаимно уничтожаются, и остается одна равнодействующая сила Р_и, параллельная и равная результирующей, но уже проходящая не через S, а смещенная относительно ее на расстояние h. Очевидно, что, вычислив по формуле расстояние h нужно это расстояние отложить от точки S на перпендикуляре к Р_и так, чтобы равнодействующая Р_и стремилась вращать тело вокруг точки S в сторону, противоположную направлению e.