Силовое исследование плоских механизмов: Методические указания к выполнению курсового проекта по дисциплине "Теория механизмов и машин", страница 6

В начале необходимо данный механизм разложить на структурные группы. Структурные группы, составляющие механизм, вычертим отдельно в масштабе, начиная с последней в порядке их присоединения. Получим структурную группу звеньев 4-5 (рис. 18,б), структурную группу звеньев 2-3 (рис. 18,в) и исходный механизм 1-го класса (рис. 18,г). Действие отброшенных звеньев в каждой группе заменяем силами реакций. При этом примем следующие обозначения: реакцию будем обозначать буквой R с двумя индексами, первый индекс обозначает номер отброшенного звена, которое производит действие, а второй индекс обозначает номер звена на которое производится действие. Например, R₁₂ - реакция 1-го звена на 2-е и т. д. Стойку будем обозначать нулевым номером, тогда, например R₀₃ означает действие стойки на 3-е звено. При этом мы учитываем сказанное в п. 5 относительно направления реакций. Реакция в шарнире, без учета сил трения, проходит через центр шарнира, реакция на ползун перпендикулярна направляющей ползуна.

Для решения задачи удобно реакции в шарнирах разложить на два направления: реакция вдоль стержня с индексом n (Rⁿ) и реакция, перпендикулярная к стержню с индексом t. Например,

.

Такое разложение показано пунктиром на рис. 18,б и в. В этом случае можно искать не полные реакции в шарнирах, а их составляющие, по которым в дальнейшем легко определить полные реакции.

Так как каждая структурная группа является статически определимой системой, то число неизвестных будет равно числу уравнений, которые можно составить для звеньев группы. Под действием внешних сил и сил реакций каждая структурная группа находится в равновесии, следовательно, векторная сумма сия, действующих на группу, равна нулю. Поэтому для каждой

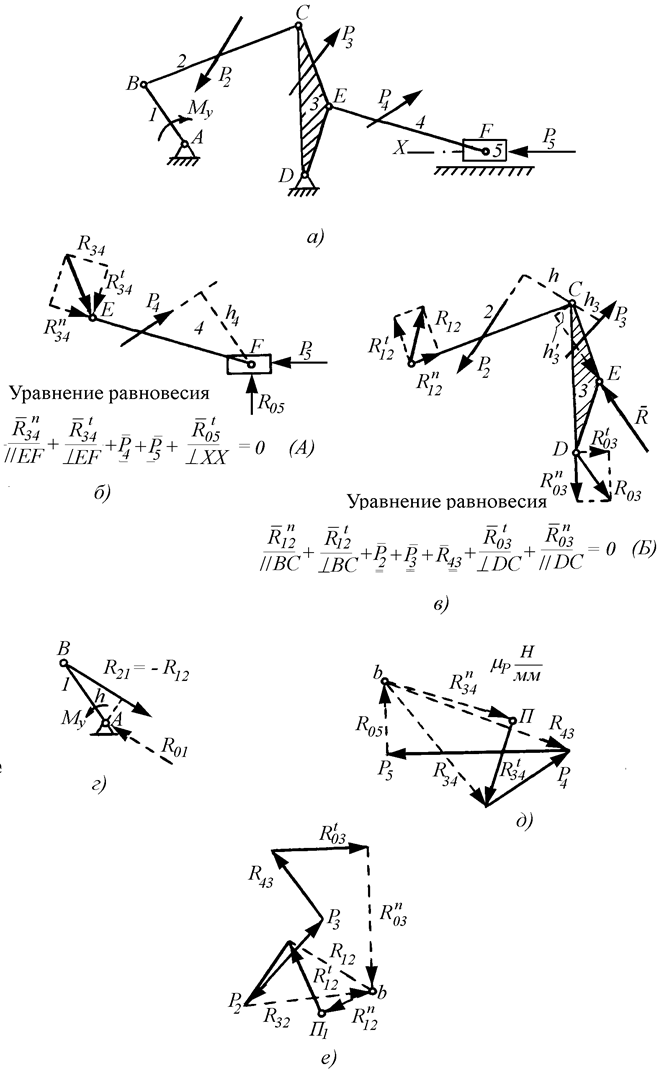
Рис. 18

структурной группы можно составить векторные уравнения равновесия (А) и (Б), которые приведены на рис. 18. В этих уравнениях известные по величине и направлению силы P₂, P₃, P₄, P₅. подчеркнуты двумя чертами снизу. Известные по направлению реакции подчеркнуты одной чертой с указанием под ней соответствующего направления. Во втором уравнении (Б) реакция R₄₃ считается известной: она должна быть равна и противоположна реакции R₃₄, которая определяется из решения уравнения (А) для группы звеньев 4-5. Иначе для структурной группы 2-3 число неизвестных будет больше, чем число уравнений, и задача будет статически неопределимой.

Из этого следует, что силовой расчет нужно начинать с последней, в порядке присоединения, структурной группы

Начиная решение задачи с уравнения (А), видим, что в этом уравнении неизвестных векторов тлеется три, в то время как графически можно решить уравнение с двумя неизвестными векторами.

В связи с этим одно из неизвестных, например,  определим из уравнения моментов всех сил, приложенных к структурной группе звеньев 4-5 относительно точки F. Имеем

,

где h₄ и EF-плечи сил относительно точки F измеряемые непосредственно по чертежу в миллиметрах. Отсюда получим:

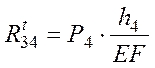, Н.

Оставшиеся неизвестные реакции  и ` определяем построением плана сил. Для этого возьмем масштаб μ_p, Н/мм, показывающий, сколько килограммов силы откладывается в 1 мм чертежа, и из произвольной точки П – полюса плана сил - будем последовательно откладывать силы, входящие в уравнение (А) (рис. 18,д).

Сначала откладываем вектор ` из его конца вектор , из конца этого вектора откладываем вектор . Из конца вектора  проводим направление вектора `, величина которого неизвестна. Так как многоугольник сил должен быть замкнут, то в полюс плана П должен попасть конец неизвестного вектора . Если через полюс П проведем направление вектора , то это направление пересечет направление вектора  в точке b плана. Эта точка и определит длины неизвестных векторов ` и `в полученном замкнутом силовом многоугольнике.