4. Моделиуправлениязапасами
Модели управления запасами по количеству включаемых в них разновидностей (номенклатур) продуктов подразделяются на две основные группы:
• однопродуктовые или однономенклатурные;
• многопродуктовые или
многономенклатурные модели управления запасами,
если модель включает
более одной разновидности сырья или продуктов.
Модель управления запасами называется детерминированной, если входящие в нее параметры являются либо константами, либо функциями наперед заданных величин. Если же хотя бы один параметр модели предполагается случайной величиной с заданным законом распределения или без такового, то такая модель называется стохастической.
4.1 Однопродуктовыемоделиуправлениязапасами 4.1.1 МодельУилсонасрасходованиемзапасовдонулевогоуровня.
При построении этой модели исходят из следующих предпосылок:
• Спрос (сбыт) в течение рассматриваемого периода Т постоянен
и объем его
на весь период известен.
• Запасы расходуются до нулевого уровня
равномерно, т.е. с одинаковой
скоростью (интенсивностью).
Самая первая поставка мгновенно восполняет первоначальный запас.
• График этой модели представлен на рис.5.
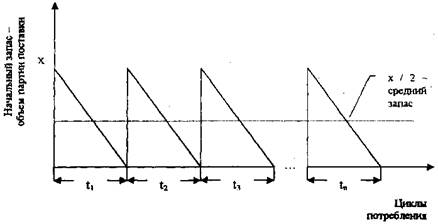
Рис.5. Модель Уилсона с мнгновенным восполнением запасов и их расходованием до нулевого уровня
Отметим, что потребление запасов, вообще говоря, дискретно. Поэтому его следовало бы изображать ступенчатой линией так, как это показано ниже (рис.6). Но здесь и в дальнейшем в целях упрощения ступенчатая линия потребления запасов заменяется прямой, соединяющей максимальный и минимальный уровень запасов.
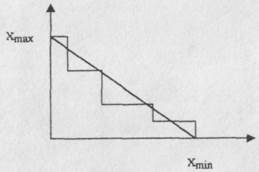
Рис.6. Условная замена ступенчатого потребления запасов непрерывным
их потреблением
Средний запас (рис.5) определяется как полусумма запасов на начало и конец цикла потребления: z = (х+0)/2=х/2.
В рассматриваемой модели заданными (постоянными) считаются следующие величины:
• Q - спрос или объем сбыта (производственного потребления) на весь период
времени Т;
• k - транспортные и другие расходы в расчете на одну партию поставки -
удельные транспортные
расходы;
• с - расходы на хранение (содержание) единицы сред'т:го
запаса в течение
всего периода времени Т- удельные складские
расходы.
Задача оптимального управления запасами в данном случае заключается в том, чтобы при оговоренных выше условиях определить такой размер заказываемой партии х°, при котором суммарные из;?*. гд:ки на поставку и хранение запасов достигали бы минимума.
Составим функцию суммарных идержек: / (n,z) = /:-п + c-z, где п - это количество поставок в течение планируемого периода 7; .: - средний запас.
Учитывая, что по определению: п = — и z = —, имеем Функцию суммарных
издержек, которая зависит только от одной переменно!, .у - объема партии поставки:
Таким образом, получаем классическую постановку задачи нахождения значения х, соответствующего безусловному минимуму функции/(It/ Найдем ее первую и вторую производные:
Ю с 2Ю
f U) = - ~ + - и /"(.г) = —р-
.г" 2 Л х
Вторая производная f"(x)>0. так как по смыслу' величины k.Q.xвсегда положительны. Следовательно, минимум функции суммарных издержек / (xtвсегда существует. Из условия минимума -• равенства нулю ее первой производной:
а,>~*и.о, ,
находим оптимальный объем поставки:
*°=J^ (4.2) V с
Это и есть известная формула Уилсона для определения оптимального объема поставки для рассматриваемой однономенклатурной модели управления запасами.
Например, при годовом объеме закупок сырья Q=J5()0 ед., издержек на доставку одной партии сырья k----8,33 О.е., издержек на содержание единицы среднего запаса с=10 д.е. в соответствии с (4.2) получаем следующий оптимальный объем партии поставки сырья:
о \2kQ '2-8,33-1500
х" = > — =---- •------- = 30 ед.
V с V 10
Зная оптимальный объем партии поставки, находим оптимальные величины остальных параметров снабжения:
_ о х 50
Средний запас z = - = — = 25 ед.;
2. 2,
Количество 0 О 1500
поставок п =-у = -^- = 30 поставок в год:
о О1500
п = •=- = — — =30 поставок в год; л-° 50
Интервал между 360 360
поставками I =—— =-- = 12 дней.
(Т-360дней) "
Именно при этих параметрах снабжения будег достигнут минимум суммарных издержек:
f° = k-n ° + с-:° = 8,33-30 + 10-25 = 500 д.е.
На практике праметры снабжения обычно отклоняются от оптимальных. Это приводит к увеличению издержек в сравнении с возможным минимумом. Обычно в управлении запасами контролируются два основных параметра: объемы и сроки поставок.
Предположим, чго в соответствии с договором поставщик обязуется поставлять рассматриваемому предприятию ингридиенты продукции - сырье, раз в месяц, т.е. через каждые 30 дней. При том же обьеме. удельных расходах па транспортировку и хранение средних запасов будем иметь следующие параметры снабжения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.