Модели управления запасами. Однопродуктовые и многопродуктовые детерминированные модели управления запасами, страница 2

Количество                  Т     ^60

поставок                 ^п = 7 ⁼ Ж ⁼ '^{2 ГЮСТаВОК В ГОД;}

1

Объем партии           __г=2₌1^ _{= 125}  единиц,

поставки                          п       12

Средний .запас             z = — = — = 62.5  ед.:

2      2

Суммарные издержки при этих параметрах снабжения составят: / > k-n   ••• с: • 8,33-12 ' 10-62.5     725д.е.,

в то время как при оптимальном варианте они составляют/ = 500 д.е. Таким образом, размер экономии издержек при оптимальном управлении запасами в сравнении с фактическим будег равен: <*f = f° -/= 500 - 725= - 125 д.е.

Минимум функции суммарных издержек в рассматриваемой модели Уилсона достигается в точке равенства величин расходов на доставку и хранение товаров. Этот факт непосредственно следует из рассмотренного выше

kO    с                   Юс

условия минимума:  /'(*) =       - + - = 0, откуда  -=•• — . Таким образом,  из

х       2                   х       2

рассматриваемого условия получаем равенство транспортных и складских расходов в точке минимума функции суммарных издержек:

«Ч <«>

Используя     данные     рассматриваемою     примера     построим     i рафик

Ш

суммарных   издержек.   Обозначим:    /, = —    иэтержки   транспортировки.

х

f₂ = с — - издержки содержания запасов.

Тогда суммарные издержки определятся как сумма двух функций:/^/} -/г , одна из которых (/}) представляет собой гиперболу, друтая - (f,) прям>то, исходящую из начала координат. Построим таблицу функций для

рассматриваемого примера, задавая значения объемов поставки х=10,20     100

(табл.6).

Таблица 6

т г                      г     ¹²⁵⁰°  _f     с

Таблица функции: fi=—    —,fi = 5x.

х

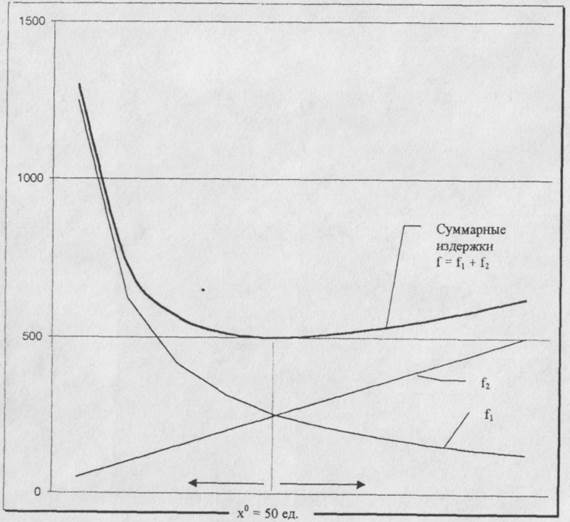
Рис. 7. График суммарных издержек для одпопродуктовой модели управления запасами

График (рис.7) отражает действие двух противоположных тенденций, а именно: снижение издержек на доставку и соответствующее увеличение издержек на содержание запасов по мере увеличения объема поставки. Оптимум достигается в точке равновесия - точке пересечения гиперболы и прямой, которой соответствует минимум суммарных издержек/⁰ = 500 д.е. и оптимальный объем поставки х° * 50 ед.

Изучая график можно видеть, что при движении влево от точки оптимума х°, т.е. при уменьшении объема поставки, суммарные издержки возрастают также, как и при движении вправо от точки .г". Но в последнем случае суммарные издержки хотя и возрастают, но значительно медленней, чем при движении влево, поскольку справа 1рафик суммарных издержек имеет более пологий вид. Отсюда следует, что если по техническим причинам нельзя точно выдержать размер оптимальной поставки, то его следует по возможности округлять в сторону увеличения, поскольку в этом случае суммарные издержки возрастут незначительно по сравнению с округлением размера поставки в меньшую сторону. В связи с этим практический интерес представляет вопрос, до каких размеров можно изменять размер оптимальной поставки не рискуя, что суммарные издержки превысят установленные пределы. Ниже предлагается следующее решение поставленной задачи.

Пусть фактический размер партии х~- ах°, где множитель а может быть больше или меньше единицы в зависимости от того, собираемся ли мы увеличивать или уменьшать фактический размер партии относительно оптимального. Запишем отношение фактических и минимальных суммарных издержек:

О       г        1 ,  Q       х°

k^ + c-      -k^- + ac~

JL«—*____ 2_ ₌ £L_*1______ 2

'' *4₊c£  *4₊,^

;c°       2          x°        2

Учитывая, что в точке оптимума издержки на транспортировку и хранение запасов совпадаю!, т.е. равны некоторому фиксированному значению

f        ~^{+al         :}     1
А = kQ/x° = cx° /2, из (4.4) получаем:                                      Отсюда

имеем    взаимосвязь   фактических    и    оптимальных    суммарных    издержек,

,.       - + а.4        2

выраженную   через  множитель  а:                   = —                         или f=Bf °      где