Модели управления запасами. Однопродуктовые и многопродуктовые детерминированные модели управления запасами, страница 4

только тремя заданными (постоянными) величинами: объемом спроса (потребления) - Q на весь планирумый период Т, удельными складскими (с) и транспортными расходами (k).

4.1.3 Модель Уилсона с допущением дефицита потребления.

Рассмотрим один цикл пофебления, в котором допускается дефицит потребления, т.е. происходит задержка поставки после того, как весь наличный запас исчерпан. Такая ситуация изображена на рис. 9.

Здесь через z обозначен начальный (максимальный) запас; /' — время
существования ненулевого запаса; I - длительность цикла потребления или
интервал между поставками; / - /' •- время отсутствия запаса или время
дефицита потребления; у  максимальный запас, необходимый для

удовлетворения спроса в данном цикле потребления; у - z - так называемый задолженный спрос или дефицит потребления.

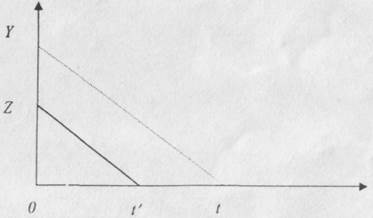
Рис.9. Цикл потребления 'запасов с допущением дефицита потребления

ГЗ дальнейшем предполагается, что за время отсутствия запасом, необходимых для удовлетворения существующего спроса, предприятия несет определенные издержки дефицита, задаваемые параметром d в расчете на единицу запаса. Это может быть упущенная выгода от перебоев в поставке производственных запасов или упущенная выгода от недореализации, если речь идет о сбытовых запасах готовой продукции.

видно   из  выражения   d = ——,   при   стремлении   уровня   обслуживания   к

\-р

максимальному (р—»1) потери от дефицита резко возрастают (d—> со).

Так, при уровне обслуживания р= 0,98 (вероятность возникновения дефицита 1 - р = 0,02) получаем d = 0,98-10 / (1 - 0,98) = 490 д.е., что в 49 раз превышает расходы на на содержание единицы товара. Другими словами, принятие более высокого уровня обслуживания, уменьшающее вероятность дефицита, значительно увеличивает издержки управления запасами.

4.2 Многопродуктовыедетерминированныемоделиуправлениязапасами

4.2.1 Раздельнаябезусловнаяоптимизацияуправлениягруппойоднородных •поназначениюзапасов.

Пусть имеется ./V однородных по назначению запасов с заданными годовыми объемами потребления по каждой позиции <2, , транспортными расходами на доставку одной партии запаса &, и расходами на содержание единицы запаса c_h где / = 1,2, ..., N. Тогда для каждой группы запасов можно провести раздельную оптимизацию, построив соответствующие им функции суммарных издержек / (xj и вычислив по формуле Уилсона оптимальные значения объемов поставки x, ° (i=l,2, ..., N). Такая оптимизация возможна, поскольку суммарные издержки по всей рассматриваемой группе запасов являются суммой издержек по каждой позиции, что дает возможность представить минимизируемую функцию в виде следующей функции многих переменных:

N                   N fcQ1  N

F(x_l,x₂,...,x_N) = Y_Jf(x_i) = ^-^!-^L+-T,^ci•*• (4.18)

;=1                  1=1    ^XiA=l

Переменные x_h x₂ , ..., x_n независимы и на них не наложено каких-либо ограничений, кроме естественного ограничения - • неотрицательности их значений. Таким образом мы имеем классическую задачу поиска безусловного минимума функции многих переменных, которую будем решать, определив частные производные по каждой переменной и приравняв их нулю:

SL.-*i2L₊l_c,,₀         (/ = 1,2,..,#)   (4.19)
dXj             x,

Из системы (4.19) для каждой позиции запасов находим оптимальные объемы

поставок:  x_t   =  I—'—-  (4.20). Остальные параметры снабжения находим по V    ^с<

известным из предьщущего формулам: z,° = х,° / 2; п° = <2,/х°; t° -Т/п°.

Минимальные суммарные издержки в целом по группе запасов определяются по формуле:

Я*ГЛ-..Д*) = Е^2*Ж (4.21). м

4.2.2 МодификациимоделиУилсона, приводящиекснижениюсуммарных издержекпогруппеоднородныхзапасов

На практике данные об издержках транспортировки и содержания запасов по каждой позиции обычно неизвестны. В связи с этим возникает задача косвенной оценки не самих показателей, а их отношения Н, = 2k, / с„ знания величины которого достаточно для определения по формуле Уилсона оптимальных объемов поставок, поскольку объемы потребления обычно известны.