Модели управления запасами. Однопродуктовые и многопродуктовые детерминированные модели управления запасами, страница 3

/°         2А2а

а² +1
В------------ множитель, показывающий, во сколько раз возрастут суммарные

2а

издержки,   если   объем   поставки   изменится   в      а-раз   по   сравнению   с оптимальными.

Преобразуем выражение множителя ft к виду квадратного уравнения:

а = /5±/Д^Т"-1    (4.5)

Выражение (4.5) позволяет установить пределы изменения размеров оптимальной поставки в зависимости от заданных пределов увеличения суммарных издержек.

Например, пусть допустимым считается увеличение издержек на 10% (рМ,1). Тогда в соответствии с (4.5):

а = 1,1 ± VU² -1 = 1,1 ± 0,4583

Следовательно, пределы изменения объема поставки будут следующими: 0,642 <а < 1,558, т.е. объем поставки можно уменьшить на 35,8% (100 - 64,2), а увеличить на большую величину 55,8% (155,8 - 100), не опасаясь, что издержки возрастут более, чем на 10%. Так, в условиях рассматриваемого примера объем ошимальной партии можно уменьшить до 32 (50-0,642), а увеличить до 78 единиц (50-1,558). При этом суммарные издержки возрастут не более, чем на 10%, т.е. не превысят 550 руб. (1,1-500).

4.1.2 МодельУилсонасрасходованиемзапасовдофиксированногоуровня.

До сих пор предполагалось, что запасы полностью исчерпываются к каждой новой поставке. Это предположение можно заменить более реалистичным: запасы расходуются до некоторого фиксированного уровня R, называемого страховым запасом, и затеме восполняются до уровня R+x. График этой модели представлен на рис.8.

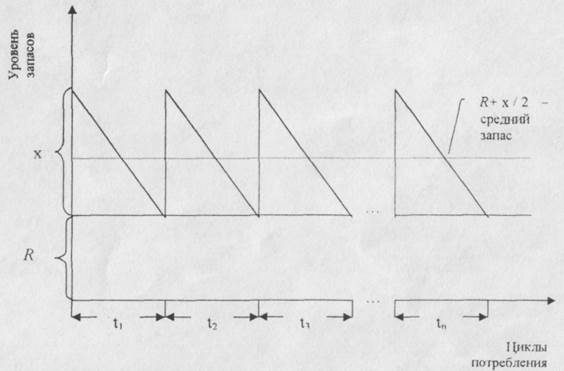
Рис.8. Модель Уилсона с мнгновенным восполнением запасов и их расходованием до фиксированного уровня

Средний      размер      запасов      в       этом      случае       будет       равен:

(R + х) + R         x

z =----------- = л н— .  Соответственно суммарные издержки  будут равны:

О           х              Ох

f(x) = k— + c(Rн—)* cR +k— + C-. Поскольку cR=const, то формула для
х             2               х

определения оптимального размера партии  будет той же.  что и в  условиях модели с расходованием запасов до пулевого уровня.

Так, если использовать данные того же примера, но предположить, что запасы расходуются не до конца, а только до контрольной точки, скажем R~30 единиц, после чего мгновенно восполняются, го объем оптимального размера партии поставки будет оставаться тем же: х° = 50 ед., однако при этом возрастет величина оптимальных средних запасов: ~° - 30 4 50/2 = 55 ео. Соответственно возрастут расходы на их содержание так. что при том же количестве поставок п° - Q / х° » 30 суммарные издержки увеличатся по

сравнению с ранее рассмотренным нулевым вариантом модели на сумму Af -cR = 10-30=300 д.е., т.е. возрастут на 60%. Таким образом, необходимость создания гарантийного или страхового запасов вынуждает предприятия нести дополнительные и довольно значительные издержки на их содержание.

Сделаем несколько замечаний, необходимых для дальнейшего рассмотрения вопроса. В рассмотренных выше моделях предполагалось, что с -это расходы на хранение единицы среднего запаса в течение всего календарного периода Т. Иногда удельные складские издержки задаются величиной с' - расходы на хранение единицы среднего запаса в день. В этом случае с = с'-Т'и формула Уилсона будет иметь вид:

' *°=JW <^4л>

В предшествующем изложении для расчета минимальных суммарных

Ю      х°

издержек  использовалась  формула:   /(* ) = — + с —.   Как  было   показано

Ж              2

kOx°.х⁰

ранее, в точке оптимума: •—- = с —. Отсюда: f(x° )=2с — = сх° . Поскольку:

х         2                                2

х° =   ——    то   минимальные  суммарные  издержки  можно  определить  по \   с

следующей формуле:

/«₌J!EL_v/2fce (4.7)

V   с

Соответственно, оптимальное количество поставок можно также определить по формуле:

„».£-    б    -Jl(4.8)

_х^йЩV2*

Из формул (4.7) и (4.8) видно, что в рассматриваемых моделях минимальные издержки и оптимальное количество поставок определяются