61.Понятие об оптимальных системах. Критерии оптимизации.
Оптимальная система- это система в которой закон управления выбран по max или min какого-либо показателя качества, при этом закон управления может быть линейным или нелинейным. Выбранные показатели качества называются критериями оптимальности. В качестве таких критериев могут быть такие параметры системы как длительность переходного процесса, производительность и экономичность и т.д.
Существуют: равномерно-оптимальные системы (каждый отдельный процесс в них является оптимальным); статически-оптимальные системы (в этих системах невозможно или не требуется обеспечить наилучшее поведение системы в каждом отдельном процессе, такие системы наилучшие в среднем); минимально-оптимальные(здесь наихудший результат лучше, чем подобный наихудший результат в любой др. системе).
1.Оптимальность по
быстродействию: критерием
оптимальности будет время переходного процесса, уравнение запишется в виде 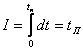 (функционал) (1)
(функционал) (1)
формулировка задачи 1: найти оптимальное управляющее воздействие и
оптимальную скорость изменения управляемой величины, которое удовлетворяет
ур.-ю объекта ![]() и обращает в min
функционал (1). При ограничениях: 1.управляющее воздействие должно быть
и обращает в min
функционал (1). При ограничениях: 1.управляющее воздействие должно быть ![]()
2. 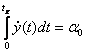 ,
система должна отработать заданный угол, т.е.
,
система должна отработать заданный угол, т.е. ![]()
3. ![]() ,
принимается для простоты решения задач
,
принимается для простоты решения задач
4. ![]()
![]() .
.
Формулировка задачи 2: существует также тип задач, где ограничения накладываются на затраты энергии, которые идут на переход системы из одного состояния в др.
Формулировка задачи такая же как и предыдущая, при ограничениях:
1. ![]()
2. 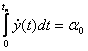 ,
,
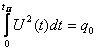 , где q0-расход
энергии.
, где q0-расход
энергии.
3. ![]()
2. Оптимальная производительность.
В этом случае критерий
оптимальности имеет вид: 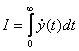 (2)
(2)
Это означает угол поворота вала двигателя за определенное время.
Формулировка задачи: найти оптимальные процессы U(t),![]() .Эти процессы должны удовлетворять
ур. объекта
.Эти процессы должны удовлетворять
ур. объекта ![]() и обращать в максимум функционал
(2).При ограничениях:
и обращать в максимум функционал
(2).При ограничениях:
1. ![]()
2. ![]() граничные
условия по скорости 0.
граничные
условия по скорости 0.
Формулировка задачи: найти оптимальные процессы U(t),![]() , которые удовлетворяют ур.
, которые удовлетворяют ур. ![]() . При ограничениях:
. При ограничениях:
1. 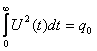 ,
если задан предельный расход энергии, а величина управляющего воздействия не
ограничена.
,
если задан предельный расход энергии, а величина управляющего воздействия не
ограничена.
2. ![]()
3. Оптимизация по экономичности.
Критерием оптимальности будет
функционал: 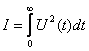 , т.е. расход энергии за определенное
время.
, т.е. расход энергии за определенное
время.
Формулировка задач: найти оптимальные процессы U(t),
скорость изменения управляемой величины ![]() ,
которые удовлетворяют ур.-ю объекта
,
которые удовлетворяют ур.-ю объекта ![]() и обращают в min
функционал I. При ограничениях:
и обращают в min
функционал I. При ограничениях:
1. 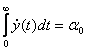
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.