Понятие об оптимальных системах. Критерии оптимизации, страница 3

Допустим уравнение имеет вид:

Вводятся обозначения:

В этом случае система уравнений записывается так:

     

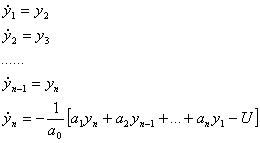
в число координат объекта включают также величину y₀, которая характеризует текущее значение функционала.

Записываем диф. ур. для координаты y₀:

             (2)

добавим уравнение (2) в уравнение (1) и запишем систему уравнений:

                   

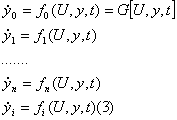
важную роль в принципе max играют следующие функции:

1. ;

2. функция Гамильтона:      (4)

  - определяется из диф. ур.

 

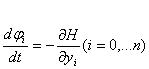
из выражения (3) и (4)такое выражение:

     (i=0,…,n)

Формулировка принципа максимума.

Для того, чтобы обеспечить оптимальность управляющего воздействия U(t) и траектории y(t) необходимо существование непрерывной функции . Эта функция должна соответствовать этим двум функциям. При этом функция  должна быть такой, что при любом (t), которое изменяется в пределах t₀≤t≤T функция Гамильтона Н достигает в точке U=U(t) максимума. Записывается в общем виде так:  

Особенностью принципа max является то, что задача нахождения функций U(t), которая обращает в экстремум функционал , заменена более простой задачей нахождения параметра U, который обращает в максимум вспомогательную функцию Н(U)

  Н

                       U_max

 

0  U

                                    extr

Алгоритм решения задач оптимизации с помощью принципа max.

1. записывают уравнение объекта в виде системы уравнений I порядка:          i=0,…n

2. составляется функция Гамильтона:

3. определяется значение управляющего воздействия U, которое образует в max функцию Гамильтона: Н=max_U1,…,Um

4. составляется совокупность уравнений для определения вспомогательных функций :      i=0,…,n

5.  через вспомогательные функции выражают искомое оптимальное управляющее воздействие.

64.Динамическое программирование Беллмана.