Понятие об оптимальных системах. Критерии оптимизации, страница 4

Ориентирован на применение вычислительной техники, т.к. имеет большой объем вычислений. Существует ряд задач когда выбор оптимального управляющего воздействия представляет собой много шаговой процесс принятия решений, т.е. процесс программирования. При этом выбор управляющего воздействия на каждом шаге осуществляется в соответствии с конечной целью управления, а также с состоянием системы, которая получена в результате решения принятого на предыдущем шаге. Пример, управление дискретными системами, которые изменяют свое состояние в соответствии с управляющим воздействием, принятым в некоторые дискретные моменты времени.

Особенность метода состоит в том, что он формирует управляющее воздействие в дискретном виде и использует уравнение объекта в конечных разностях вместо диф. ур. Этот метод может применяться для решения задач управления как непрерывными так и дискретными процессами. Для численного решения непрерывных задач приходится заменять непрерывный процесс дискретным. Эта замена осуществляется с интервалом, который зависит от требуемой точности решений. Однако для оптимизации непрерывных систем этот метод применяется реже, чем принцип max, это связано с тем, что не всегда существуют частные производные от функционала. Наибольший эффект при применении этого метода дает оптимизация дискретных систем.

Формулировка принципа оптимальности Беллмана: в текущий момент времени необходимо принимать такое управляющее решение, чтобы достичь наилучших результатов за оставшееся время.

Использование этого принципа позволяет решение сложной задачи многошагового управления заменить на последовательное решение нескольких более простых одношаговых задач.

Рассмотрим смысл принцип оптимальности t₀≤t≤t_К

                           y                         

   y₀

                                                    y_к

требуется осуществить оптимальный по быстродействию перемещение объекта из y₀ в y_{конечное}.

         - уравнение оптимальной траектории.

общее время

  (1)

смысл уравнения (1), т.к. y(t)-оптимальная траектория, то для любой промежуточной точки заключительный участок траектории также является оптимальной траекторией.

 

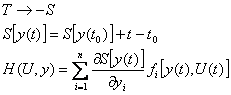
 - оптимальность процесса достигнута, ур.-е Беллмана.

Точное решение уравнения Беллмана является трудным, применяют численные методы.

Последовательность применения метода Беллмана.

   (2)

, 

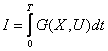
диф. уравнение (2) заменяется приближенным разностным уравнением: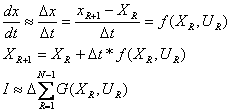

в результате будет найдено условное оптимальное решение U_N-1.