Понятие об оптимальных системах. Критерии оптимизации, страница 2

2.

62.Классическое вариационное исчисление.

Обычно применяется для решения задач с нелинейными функционалами и условиями в виде нелинейных функций. В отдельных случаях может быть использован в случае нелинейных функционалов и условий: 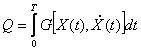 (1)

Найти Х(t), который превращает в экстремальное значение функционал (1). Для этого записываем ур.-е Эйлера:

, ,

метод Эйлера предполагает, что все четыре функции являются непрерывными: .

W

                                 U                    X

Возможны две разновидности задач:

1. когда ур. связи имеет вид,     (2)

в этом случае используется метод неопределенных множителей Лагранжа, который состоит в том, что ур.-е Эйлера записывается для вспомогательной функции.      (3)

- множители Лагранжа, которые надо найти.

 

X(t)                            все это находят из системы уравнений

X₁(t),…,

В эту систему входят ур. Эйлера для функции (3), а также совокупность уравнений связи вида (2).

Такая задача называется общей задачей Лагранжа.

2. второй случай задачи управления: в этом случае уравнение связи задается в виде интеграла, 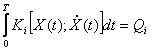     (4)

i=1,…n   ; Q_i- заданные величины.

В этом случае для решения задачи составляется вспомогательная функция.

            (5)

задача управления при условиях вида (4)называется изопериметрической задачей Лагранжа. В данном случае для нахождения функции X(t) и множителей Лагранжа , используют уравнение Эйлера для функции (5) и уравнение связи вида (4)

63.Принцип максимума Понтрягина.

Наиболее эффективен при решении линейных задач, когда на управляющее воздействие или на координаты наложено ограничение в виде неравенств. Принцип max применяется для систем управления, поведение которых описывается системой диф.ур. I порядка. Эта система выглядит так:

    (1),   i=1,…n

ставится задача найти управляющее воздействие U(t), переводящая систему за время Т из положения y(t₀)       y(T). При этом должно обеспечиваться экстремальное значение следующего функционала:

                                                                                         

переход к описанию объекта управления в виде системы уравнений (1) от лин.ур. I порядка производится путем замены соответствующих переменных и подстановки их в исходное уравнение.