3. НЕКОТОРЫЕ ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
3.1. Классификация методов идентификации динамических систем
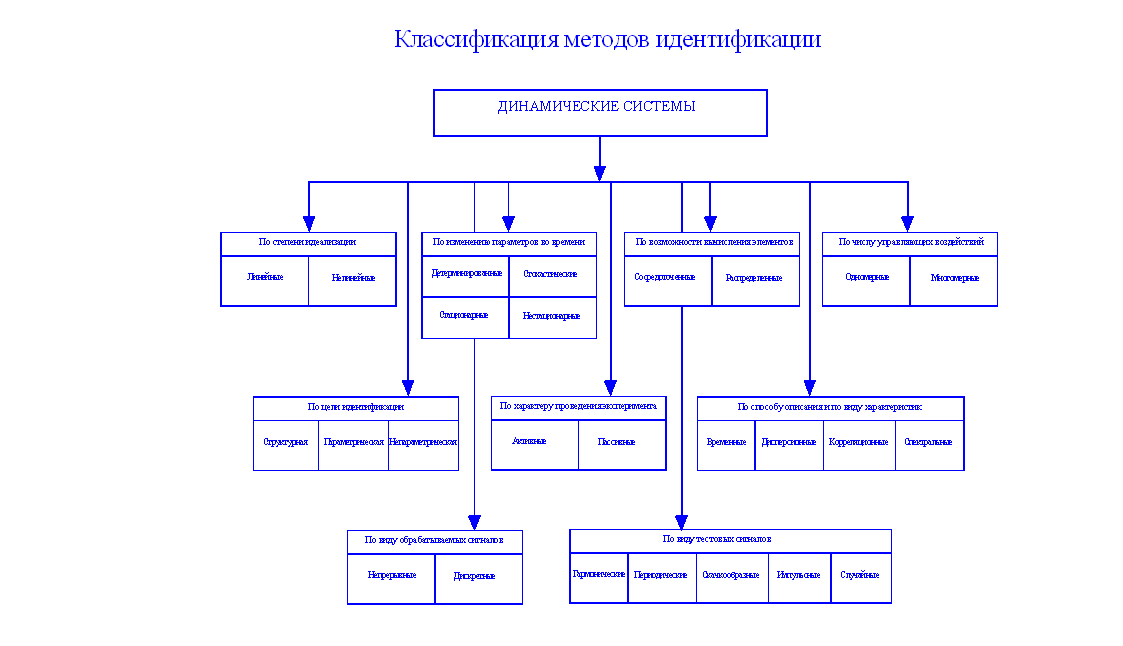
С целью определения области исследования рассмотрим классификацию методов идентификации динамических систем и признаков, по которым она проводится (классификация приведена на рис. 3.1.).
В общей постановке проблема идентификации состоит в отыскании некоторого формализованного (математического или логического) описания, несущего информацию о динамических свойствах объекта (системы). Эта информация должна быть достаточна для осуществления целей управления и для решения поставленных задач синтеза оптимальных параметров системы.
Различают идентификацию в широком и узком смысле. В задачу идентификации в широком смысле входит анализ структуры системы, установление формы аналитического описания процесса и определение основных его параметров. При идентификации в узком смысле оцениваются только параметры.
При идентификации большая роль отводится концептуальному выбору класса системы и степени ее структурной сложности. Так как класс системы определяет наиболее общие формы ее описания, то приведем основные признаки их классификации. По степени идеализации и по виду описания операторных уравнений системы разделяют на линейные и нелинейные динамические системы. К линейным относят класс систем, который описывается линейными операторными уравнениями, частным случаем которых являются линейные дифференциальные и разностные уравнения, а также их системы. Все остальные системы, которые не подходят под класс линейных , определяются в классе нелинейных систем. Так как линейные системы подчиняются принципу суперпозиции и способы описания процессов внутри таких систем широко исследованы, то их идентификация в большинстве случаев сводится к поиску оптимальных методик и алгоритмов, обеспечивающих успех применения разработанных с их помощью моделей на практике. Нелинейные системы, напротив, не подчиняются принципу
|
суперпозиции, и их идентификация вызывает существенные затруднения. К настоящему времени разработано большое количество методов и подходов к идентификации нелинейных систем. В основном эти методы, в зависимости от степени нелинейности, определяют нелинейную систему в класс квазилинейных систем с использованием методов гармонической линеаризации или представлением систем с помощью функциональных рядов Вольтера, Гаммерштейна, Винера и Винера – Гаммерштейна. Такие ряды описывают нелинейные динамические системы, образованные различными комбинациями линейных динамических звеньев и безынерционных нелинейных элементов. К таким системам относят также системы типа фильтров Заде и обобщенную модель Винера.
По изменению параметров системы во времени различают детерминированные и стохастические системы. В свою очередь эти два вида систем разделяют на стационарные и нестационарные динамические системы. К классу стационарных систем относят такие системы, у которых коэффициенты дифференциальных уравнений вне зависимости от режима работы системы являются постоянными. К нестационарным системам относят те системы, поведение которых описывается дифференциальными уравнениями с переменными коэффициентами. Определение системы в класс стационарных систем намного облегчает идентификацию. Если система нестационарна, то такую систему для каждого режима работы или интервала времени, в котором коэффициенты дифференциальных уравнений постоянны или изменяются на незначащую величину, разбивают на подсистемы и относят к классу квазистационарных систем. Для каждой такой подсистемы проводят отдельную идентификацию подобно стационарной системе. В настоящее время также для идентификации нестационарных динамических систем используются методы, базирующиеся на Вейвлет–преобразовании.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.