(3.15)
(3.16)
где N – количество отсчётов во временном ряду.
3.4. Цифровые методы регулирования систем управления
В предыдущих главах мы рассмотрели вопрос об идентификации систем. Рассматривалась разомкнутая система, в которой регулятор (или регуляторы, как в случае многосвязной системы) отключён (отключены). Это, возможно, допустимо на непродолжительное время, достаточное для идентификации системы, однако в реальных условиях регулирование должно осуществляться всегда, чтобы технологический процесс удовлетворял требуемым параметрам качества. Необходимо каким‑нибудь образом подключить регуляторы к системе.
Кроме того, важной задачей автоматизации является обеспечение оптимальных (в каком‑либо смысле) настроек регулятора (или – опять же – регуляторов, как в нашем случае). Часто эта задача имеет весьма непростое и, что немаловажно, далеко неоднозначное решение, причём, чем сложнее система, тем труднее подобрать настройки, удовлетворяющие заданным требованиям.
В данной работе, из‑за недостатка времени, вопрос об оптимальных настройках рассмотрен не был. Мы ограничились тем, что реализовали цифровое регулирование нашей многосвязной системы. То есть в роли регулятора выступает ЭВМ, а не какая‑нибудь электрическая или пневматическая, или ещё какая иная схема. Естественно, с учётом того, что в качестве системы мы использовали всего лишь её электрическую модель, наша задача значительно упростилась: нет проблем с преобразованием электрического сигнала – выходного сигнала регулятора – в сигнал какой‑нибудь другой природы, что вносило бы какие‑то помехи – упрощений хватает.
Все системы регулируются сходным образом и его можно представить так, как показано на рисунке.
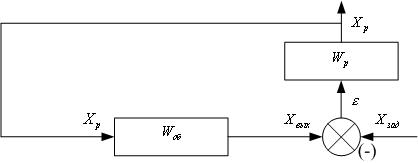
Рис. 3.4. Схема регулирования.
Нас в данном случае
интересует участок 
, в котором 
‑ ошибка регулирования, 
‑ регулирующее воздействие, а 
‑ передаточная функция регулятора, которая имеет вид:
(3.17)
Данное изображение характеризует ПИД‑регулятор непрерывного типа. Нам же требуется осуществлять регулирование с помощью ЭВМ, то есть цифровым методом. Чтобы перейти к цифровому методу, необходимо найти дискретную передаточную функцию. Переходя к Z‑преобразованию (по формуле Гастина), получаем следующие результаты:
, (3.18)
здесь 
‑ дискретность.
Далее необходимо перейти к разностному уравнению:
,
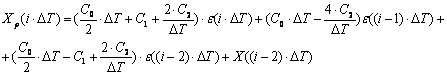(3.19)
здесь i – номер текущей точки.
Трудности, возникающие при определении оптимальных настроек регулятора в многосвязных системах
Немного выше мы уже рассказали вкратце о сложности подбора настроек, удовлетворяющих заданным критериям качества. Коснёмся этого вопроса чуть подробнее. Итак, рассматривается система с регуляторами.
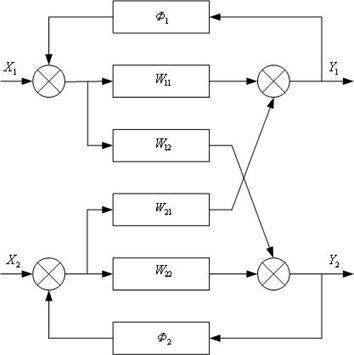
Рис. 3.5. Многосвязная система.
Здесь:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.