Классификация методов идентификации динамических систем, страница 3

1)  плотности распределения вероятностей имеют удобный для аналитических исследований вид;

2)  случайный шум несёт в среднем равные мощности на всех частотах;

3)  для данного уровня постороннего шума очень удобно проводить осреднения и по отрезкам ряда соответствующей длины, и по частотам в достаточно широких диапазонах, что даёт возможность увеличивать статистическую устойчивость и повышать тем самым точность оценок;

4)  использование  случайного шума одной из составляющей входного сигнала применимо как для активной  идентификации, так и для пассивной;

5)  применение быстродействующих ЭВМ и аналогово–цифровых систем заложило прочную практическую основу под данную методику.

Методы идентификации разделяют по способу описания процессов в системе, а также по виду характеристик, используемых при их реализации. Различаются временные, дисперсионные, корреляционные и спектральные методы идентификации. Среди этих методов важное место занимают корреляционные и спектральные методы идентификации. Они обеспечивают высокую помехозащищенность и статистическую устойчивость, а также дают возможность проведения экспериментов в режиме нормальной эксплуатации объектов.

С целью сужения области исследования рассмотрим идентифицируемую систему в совокупности с представленными выше методами и их признаками.

3.2. Идентификация одномерной линейной системы методом наименьших квадратов.

Рассматривается одномерная линейная система, на которую подаём зашумлённый сигнал.

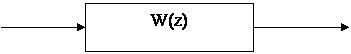                          X(iT)                                       Y(iT)

рис.1 Схема одномерной системы.

Над передаточной функцией W(p) проводим Z-преобразование, и серию выходных сигналов аппроксимируем разностным уравнением вида:

                                (3.1),

где N – порядок передаточной функции;

T – дискретность.

a_k, b_k – коэффициенты, которые необходимо найти.

Если k>i, то сигнал равен нулю (его ещё не существует).

Для нахождения коэффициентов a_k, b_k воспользуемся методом наименьших квадратов.

       (3.2),

Здесь J – сумма ошибок между расчётными и экспериментальными точками. Важно отметить, что вместо расчётной точки в формуле берём экспериментальную – ведь расчётная нам ещё не известна, мы найдём её, когда определим коэффициенты a_i, b_i. Для нахождения коэффициентов нам необходимо составить систему уравнений, исходя из соотношений:

                                                                          (3.3),

Матрица  будет иметь следующий вид:

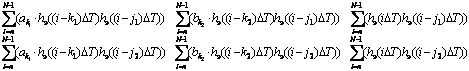    (3.4)

Здесь:

k₁, j₁ меняются от нуля до n (производные по коэффициентам при X).

k₂, j₂ меняются от единицы до n (производные по коэффициентам при Y).

Таким образом, получается матрица размерностью (2n+1)*(2n+2), причём последний столбец, в формуле он третий, ‑ столбец свободных членов.

Данную линейную систему можно решить разными способами, например, как это сделали мы ‑ методом Гаусса, хотя нельзя сказать, что этот метод безупречен: если система не имеет решения, то коэффициенты не будут найдены.

Итак, система имеет решение, коэффициенты найдены, получена некоторая функция, аппроксимирующая заданную с достаточной точностью. Необходимо получить передаточную функцию по Лапласу (так называемая параметрическая идентификация), но прежде необходимо найти Z-преобразование передаточной функции.