Классификация методов идентификации динамических систем, страница 4

Для этого воспользуемся свойством Z-преобразования:

                                (3.5)

Соответственно, Z-преобразование передаточной функции будет иметь вид:

                                                                       (3.6)

Прежде чем перейти к преобразованиям Лапласа, напомним формулу Гастина:

                                                                                    (3.7)

Зная вышеприведённую формулу, легко проверить, что:

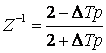                                                                                     (3.8)

Подводя итоги, представим схему идентификации.

                   рис. 3.2 Схема идентификации

3.3. Идентификация многосвязной системы методом наименьших квадратов.

 

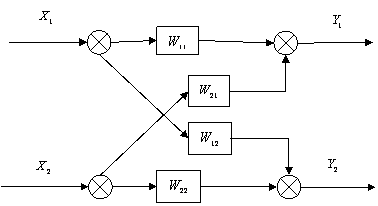
         рис. 3.3 Двухсвязная система управления.

Выходы зависят от входов друг друга, что существенно усложняет исследование и регулирование системы.

Взаимосвязь между выходными и входными сигналами двухсвязной системы (рис. 3.3) может быть описана линейными дифференциальными уравнениями следующего вида:

                                                (3.9)

                                                         (3.10)

Для дискретного аналога непрерывной динамической системы уравнения (3.9), (3.10) заменяются линейными разностными уравнениями:

                                   (3.11)

                                  (3.12)

Выражения (3.11) и (3.12) могут быть представлены в виде удобным для моделирования, а именно:

                                                                                  (3.13)

                                                                     (3.14)

Параметрический анализ во временной области предполагает оценивание параметров …, …, …, …, …, …при известных порядках n₁ и n₂ модели.

Как правило, порядок модели неизвестен, поэтому число параметров, описывающих динамические свойства системы, определяют экспериментально, увеличивая количество членов в левой части выражениях (3.13) и (3.14) до тех пор, пока автокорреляционная функция остаточных ошибок не будет информировать нас о том, что нет признаков корреляции остаточных ошибок.

Параметры …, …, …, …, …, …при фиксированных значениях n₁ и n₂ могут быть определены с помощью метода наименьших квадратов, который минимизирует сумму квадратов отклонений выходных значений  и , измеренных экспериментально, от расчетных, полученных из выражений (3.13) и (3.14). Для идентификации параметров данной системы этот метод будет иметь следующий вид: