Аппроксимация переходной характеристики объекта, страница 9

2) первый максимум:

3) второй максимум:

4) σ – перерегулирование, max отклонение переходной характеристики от          

   установившегося значения выходной величины, выраженное в %

                           

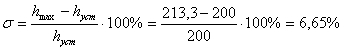
5) время достижения первого max 

6) время достижения второго max 

7) период колебаний

8) частота колебаний

9) n – число колебаний, количество колебаний, которое имеет переходная характеристика за время tp, допускается 1-2 колебания.   n=9

10) время нарастания ПП, абсцисса первой точки пересечения переходной характеристики с уровнем установившегося значения. 

11) степень затухания переходного процесса

                         

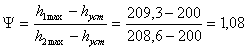
12) Интегральный критерий качества:

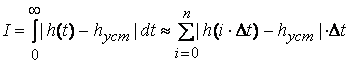
где – дискретность (принимаем равным 0,12)

        n = t/ – количество интервалов разбиения на всём рассматриваемом участке переходной характеристики:

с

Таким образом получаем:

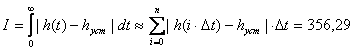
Расчёт оптимальных настроечных параметров регулятора методом РАФЧХ.

1. Получим РАФЧХ объекта регулирования путем замены оператора Лапласа р на (j – m):

 - исходная передаточная функция

- РАФЧХ объекта

В полученном выражении выделяем мнимую и вещественную части:

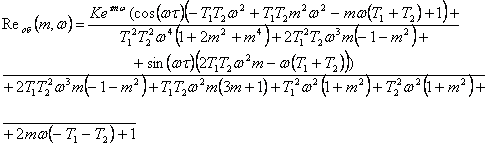
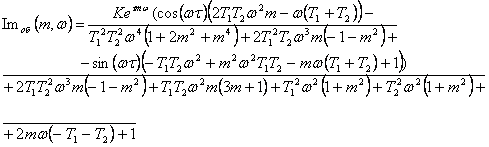
подставим значения:

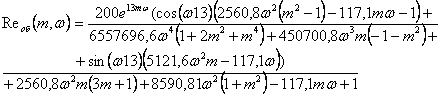
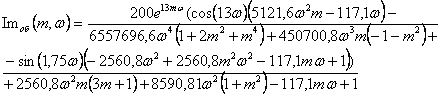
2. Аналогичным образом находим РАФЧХ регулятора:

- передаточная функция ПИ-регулятора

где

С₁=К_р – коэффициент передачи (пропорциональности) регулятора (П-составляющая)

С₀=К_р/Т_и ( Т_и – время интегрирования) И-составляющая

- РАФЧХ регулятора

3. Исходя из условия:

получаем следующее:

Преобразуем полученное равенство в систему уравнений:

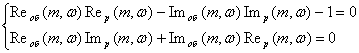
Решаем систему уравнений относительно  и , получаем: