Аппроксимация переходной характеристики объекта, страница 10

Таким образом, получаем следующую систему уравнений:

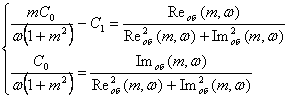
Решая полученную систему, получаем:

где  и  были определены ранее.

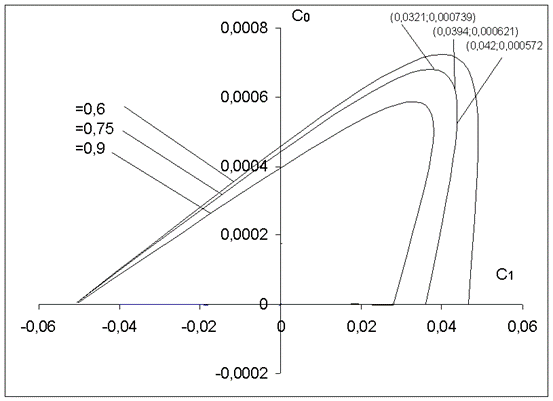
4. Построим в координатах С₀ и С₁ зависимость С₀ = f(С₁), меняя частоту  от нуля до значения при котором величина С₀ становится отрицательной:

Выбираем степень затухания  = 0,75, таким образом, степень колебательности m будет равна:

На графике выбираем точку, которая находится немного правее максимального значения  С₀  и имеет параметрами С₀ = 0,000621 и С₁ = 0,0394.

В соответствии со значениями С₀ и С₁ находим время интегрирования Т_и и коэффициент передачи регулятора:

K_Р. = С₁ = 0, 0394

Т_и = К_р/С₀ = 0,0394/0,000621 = 63,4с

В соответствии с полученными параметрами строим переходной процесс замкнутой САР.

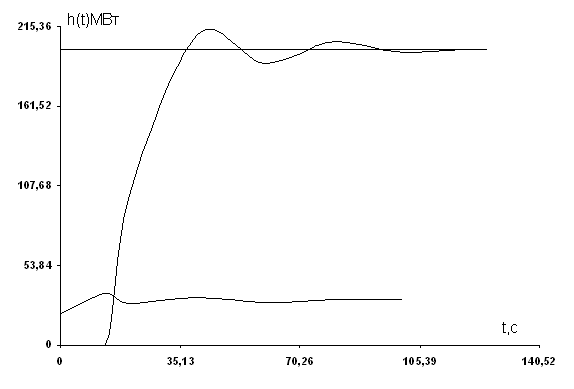
. 1 – переходной процесс в замкнутой САР;

2 – входная величина регулятора.

3 – выходная величина регулятора;

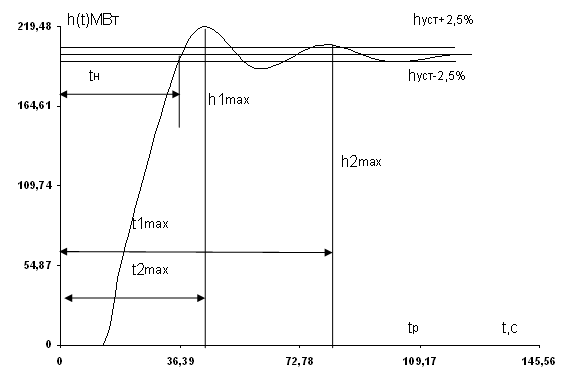
Оценим качество полученного переходного процесса:

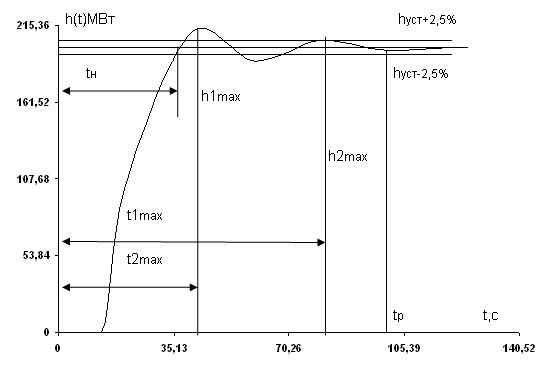
1) Время переходного процесса: t_p = 98,8с

2) Первый максимум: h_1max = 215,36об/мин

3) Второй максимум: h_2max = 205,96 об/мин

4) Перерегулирование:

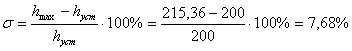
5) Время достижения 1-го максимума: t_1max = 42,25с

6) Время достижения 2-го максимума: t_2max = 80,6с

7) Период колебаний: T = t_2max  - t_1max = 80,6– 42,25 = 38,35c

8) Частота колебаний:

9) Число колебаний: n =2

10) Время нарастания переходного процесса: t_H = 36,4с

11) Степень затухания переходного процесса:

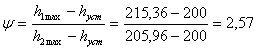
12) Интегральный критерий качества:

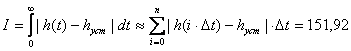
На графике выбираем точку, которая соответствует максимальному значению С₀ с параметрами С₀ = 0,000739 и С₁ = 0,0321

В соответствии со значениями С₀ и С₁ находим время интегрирования Т_и и коэффициент передачи регулятора:

K_р = С₁ = 0,0321

Т_и = К_р/С₀ = 0,0321/0,000739 = 43,4с

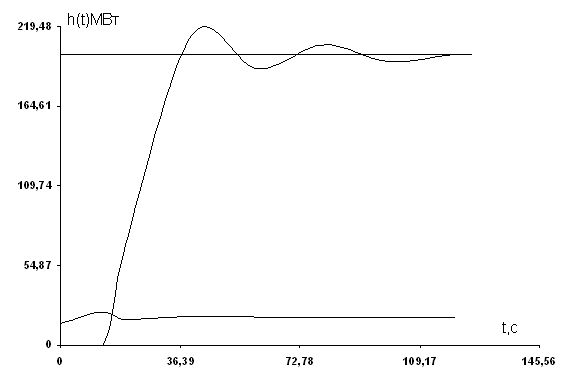оценим качество полученного переходного процесса

1) Время переходного процесса: t_p = 103,1с

2) Первый максимум: h_1max = 219,48