Сложная многосвязная электроэнергетическая система, страница 8

Величина полного тока , в этом случае, в соответствии с рис.2.5.2. может быть определена как:

.

Тогда:

                      .                             (2.5.25)

Очевидно, что модуль этой ЭДС равен E_Q и может быть найден по формуле:

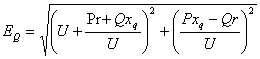.                                     (2.5.26)

Аргумент ЭДС E_Q определяется как:

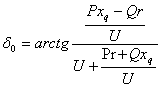.                                         (2.5.27)

 

                                                       [7]           _{.  .}                       [6]

                                                            U_d Iz_{q       .}

                                   [9]          d₀       U             Ix_q

                                     I_a=P/U       [1]                       [11]

                      0        j          [2]                   [5]

                                       -U_d [8]

                                  [3]                      [4]

                                     [10]

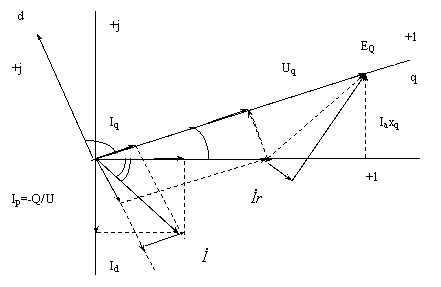
Рис. 2.5.2. Векторная диаграмма синхронной машины

После нахождения величины и положения на комплексной плоскости ЭДС E_Q, а следовательно, и направления поперечной оси ротора синхронной машины могут быть найдены q, d - составляющие всех переменных. Для нахождения  q, d - составляющих векторов тока могут быть использованы следующие формулы:

                                  (2.5.28)

Таким образом, при известных параметрах синхронной машины x_q,x_d , имея в качестве исходных данных параметры

d₀      ,

по соотношению (2.5.28) могут быть рассчитаны искомые токи установившегося режима в статорной цепи I_q и I_d, а следовательно и остальные параметры, y_q, y_r, E_q   и т.д.

При исследовании установившегося режима возможна обратная ситуация, когда по известным d₀, I_q , I_d, E_q, U необходимо вычислить активную (Р) и реактивную (Q) мощности генератора. Воспользуемся соотношением (2.5.25) и выразим из него  P и Q через остальные переменные, для простоты пренебрегая активным сопротивлением r, полагая Z=jx_d:

.                                           (2.5.29)

Напомним, что вектор U совмещен с вещественной осью. E_a и Е_р - соответственно проекции вектора  на действительную и мнимую оси. Домножим обе части (2.134) на U и кроме этого, числитель и знаменатель правой части на (-j):

                                         (2.5.30)

или:

    .                                               (2.5.31)