Система семи уравнений Горева-Парка (2.2.19) есть совокупность нелинейных дифференциальных уравнений движения синхронной машины. Для применения упомянутых выше стандартных математических методов анализа и синтеза ее необходимо линеаризовать.
2.3 Необходимость линеаризации систем
Отметим еще раз, что все выводы по использованию традиционных моделей и методов синтеза желаемых динамических свойств (п.1.3) справедливы только для линейных систем, в уравнения движения которых, входят переменные только в первой степени.
Из соотношений (2.2.19) следует, что некоторые уравнения
движения электрической системы нелинейны, поскольку включают произведения и
тригонометрические зависимости переменных, характеризующих состояние системы. Например,
взаимные произведения переменных состояния (
и 
).
Для применимости хорошо разработанного аппарата
исследования и синтеза линейных систем исходные дифференциальные уравнения
необходимо линеаризовать в некоторой области исследуемого режима. Для этого
необходимо рассчитать совокупность нормальных предполагаемых режимов работы
системы. (Например, один из них характеризуется параметрами 
). Тогда 7-ое уравнение в результате
линеаризации будет выглядеть:
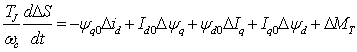(2.3.1)
Заметим, что данное уравнение записано уже относительно отклонений переменных в области рассчитанного режима.
Ниже будет показано, что нелинейная составляющая в седьмом уравнении системы (2.2.19), при традиционных аналитических исследованиях, трансформируется в нелинейную зависимость ЭДС (EQ) и напряжения шин (U), включающую тригонометрическую функцию от электрического угла (δ). При этом седьмое уравнение (2.2.19) приобретает вид:
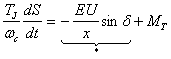, (2.3.2)
где нелинейная составляющая (*) является выражением для активной мощности генератора:
.
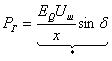(2.3.3)
Соотношение (2.3.3) называется угловой характеристикой активной мощности генератора и играет важную роль при анализе устойчивости системы. Для упрощения анализа переходных процессов в ЭЭС необходимо прибегать к методу линеаризации вблизи рабочей точки режима. Суть его в том, что нелинейные зависимости параметров друг от друга аппроксимируются касательной прямой в некоторой точке "а" (рис.2.3.1).
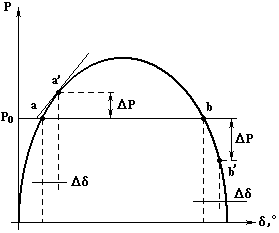
Рис. 2.3.1. Пример линеаризации в рабочей точке угловой
характеристике мощности
Точка "а" определяет установившийся режим системы. Если предположить, что возмущения приводят к незначительным отклонениям режима от рабочей точки, то нелинейная зависимость в области этих отклонений между активной мощностью, ЭДС и электрическим углом (2.3.3), может быть заменена на линейную:
, (2.3.4)
где K1, K2 - коэффициенты пропорциональности, зависящие от режима (от расположения рабочей точки на угловой характеристике). В, частности, изменяющимися параметрами в (2.3.3-2.3.4) являются EQ и d. Значения Uш и xГ заданы и неизменны. Пусть рабочий режим генератора выбран и характеризуется значениями переменных EQ= EQ0; d=d0 тогда линеаризация нелинейной зависимости осуществляется с использованием частных производных, вычисленных в точке рабочего режима:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.