Сложная многосвязная электроэнергетическая система, страница 7

2.5. Уравнения  установившегося режима синхронной машины

Формально уравнения установившегося режима (УР) синхронной машины могут быть получены из системы (2.2.19) вычеркиванием всех членов, содержащих производные величины во времени:

1.                                                                            (2.5.14)

2.                                                                             (2.5.15)

7.                                                                 (2.5.16)

Нумерация слева - соответствует принятой для исходной системы уравнений движения (2.2.19). На рис. 2.5.1 показаны проекции вектора напряжения, со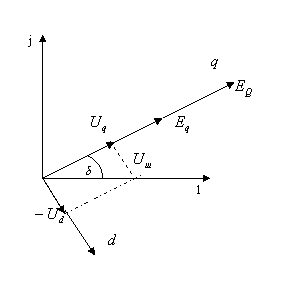вмещенного с синхронно вращающейся действительной осью (1) на оси  q и d.

  

Рис. 2.5.1  Векторная диаграмма напряжений в установившемся режиме

В соответствии с рисунком для проекций векторов справедливы следующие соотношения:

;                                                                       (2.5.17)

   ;                                                                     (2.5.18)

 .                                                                     (2.5.19)

Запишем  и проанализируем вначале уравнения УР в  статорных цепях синхронной машины, вытекающие из первого и второго уравнений движения (все переменные описывающие УР будем обозначать прописными буквами):

1. ;                                                                         (2.5.20)

2. .                                                                          (2.5.21)

Прежде чем преобразовать уравнения (2.5.20) и (2.5.21) введем понятие фиктивной ЭДС E_Q,, связанной с E_q  соотношением:

 .                                                                       (2.5.22)

Заметим, что для неявнополюсных машин (например, турбогенераторов, у которых статорные обмотки симметричны  ) . Это обстоятельство позволяет утверждать, что вектор ЭДС E_Q  должен совпадать по направлению с поперечной осью q (рис.2.5.1).

Исключим из первого уравнения (2.5.20)  E_q ,  заменив ее соотношением (2.5.22). Затем, домножим второе уравнение (2.5.21) на (-j) и сложим с первым. В результате преобразования получим:

               ,                                        (2.5.23)

или короче :

                                 .                                                  (2.5.24)

Выражения (2.5.23) и (2.5.24) проиллюстрированы векторной диаграммой установившегося режима СМ на рис. 2.5.2.

Таким образом, используя ЭДС E_Q , можно представить синхронную машину в установившемся режиме ее работы в виде ЭДС, включенной за сопротивлением Z_q (при пренебрежении r, за x_q).  Очевидно, что выражение (2.128), записанное при использовании комплексной плоскости, вещественная ось которой совмещена с осью q, а мнимая - с осью d, будет справедливо при любом другом положении осей комплексной плоскости. В частности, удобно совместить вектор напряжения U с вещественной осью новой комплексной плоскости  (рис.2.5.2).