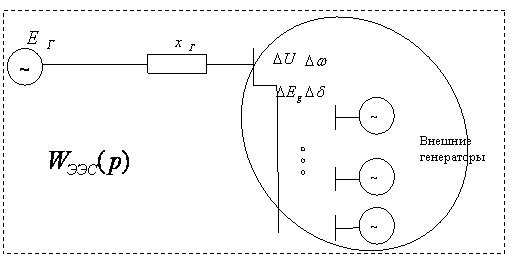
Рис.2.1.2. Обобщенное представление сложной ЭЭС относительно одного из эквивалентных генераторов, при отсутствии регулятора
Как следует из рис.1.2.1 (п.1.2), без значительных
допущений и упрощений можно утверждать, что исходная сложная
электроэнергетическая система, которая в итоге представлена математическим
эквивалентом в виде ПФ 
, относительно одного из
эквивалентных генераторов, при отсутствии регулятора, имеет обобщенный вид
(рис.2.1.2). На этом рисунке кривая замкнутая линия объединяет все внешние по
отношению к исследуемому эквивалентному генератору элементы, включая
распределительную сеть.
Существуют формальные методы упрощения структуры внешней электрической сети, путем сворачивания ее и замены групп параллельных, последовательных, треугольных и др. соединений элементов эквивалентными [ ]. Наиболее глубокий уровень эквивалентирования внешней сети приводит к замене ее внешним сопротивлением эквивалентной линии XЛ (рис.2.1.3).
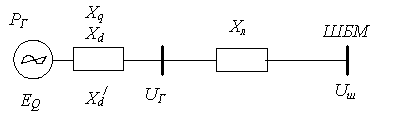
Рис.2.1.3. Схема замещения простейшей эквивалентной электрической системы (электропередачи)
В отличии от подхода, при котором итоговая эквивалентная передаточная функция определяется по совокупности составляющих ПФ и ЧХ, в данном случае этап эквивалентирования выполняется не для структурной схемы системы, а для электрической. Такой подход широко используется среди специалистов энергетиков в задачах управления электрическими режимами и устойчивостью ЭЭС.
Простейшая электрическая система, схема замещения, которой приведена на рис.2.1.3 называется электропередачей. Она часто используется в качестве модели энергосистемы, когда необходимо подробно учесть электрические свойства эквивалентного генератора при исследовании процессов, протекающих в сложной системе.
При использовании данной модели часто делаются некоторые допущения, в частности: отсутствуют активные составляющие электрических сопротивлений, потери активной и реактивной мощности в линии и ее поперечные проводимости [Жд]. Эти допущения незначительно искажают количественные результаты исследований переходных процессов в системе, но полностью сохраняют качественные закономерности связи регулирующих воздействий с динамическими свойствами системы. Очевидно, при использовании стандартных методик исследования динамических свойств системы и соответствующего программно- математического обеспечения указанные допущения необязательны. Однако, благодаря им, возможно проведение в учебных целях аналитических исследований, раскрывающих физические основы протекающих процессов.
2.2. Математическое описание синхронной машины. Семь уравнений движения
Вернемся к описанию простейшего элемента сложной системы в соответствии с рис.1.2.3 – 1.2.4 (п.1.2). Как показано выше, таким элементом является электропередача (рис.2.1.3). Схему замещения электропередачи можно легко свести к схеме замещения вращающейся машины (рис.2.2.1). Наиболее общее математическое описание из машин имеет синхронная (синхронный генератор). Именно ее будем рассматривать в качестве простейшего элемента, имея в виду, что модели остальных машин, являются частным случаем.
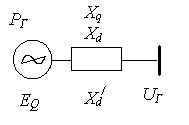
Рис.2.2.1. Структура уравнений движения и схема замещения синхронной машины
Рассмотрим кратко традиционную математическую модель синхронной машины в виде семи дифференциальных уравнений движения, построенную при использовании законов Кирхгоффа, применительно к неподвижным и вращающимся электромагнитным контурам статора и ротора [ ].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.