Сложная многосвязная электроэнергетическая система, страница 3

При записи уравнений используется прямоугольная вращающаяся с синхронной частотой ()  система координат q , d []. Запишем уравнения (1 и 2, рис. 2.2.1) статорных цепей СМ во вращающейся системе координат q, d:

1.                                                          (2.2.1)

2.                                                          (2.2.2)

Они записываются исходя из первого закона Кирхгоффа, применительно к сумме проекций на каждую из осей q и d падений напряжения в статорной цепи. В частности, первая составляющая в каждом из уравнений определяется активным сопротивлением обмотки статора, вторая – индуктивным, третья – величиной ЭДС, возникающей при взаимном перемещении магнитных полей статора и ротора. Четвертая составляющая – ЭДС (e),  наводится в статорной обмотке током ротора, при этом:

                           ,                                             (2.2.3)

где:             y₀ - вектор потокосцепления статора, обусловленный действием контура возбуждения;  i_r - ток в обмотке возбуждения;   M_d - коэффициент взаимоиндукции между обмоткой возбуждения и обмоткой фазы статора, при совпадении их магнитных осей.

Тогда из (2.2.3) и условия вращения обмотки ротора с частотой w имеем выражения для составляющих e_q и e_d:

               .                                           (2.2.4)

Вернемся теперь к исходным уравнениям (2.2.1-2.2.2) и преобразуем их с учетом следующих обозначений.

Введем индуктивное сопротивление фазы статора при синхронной частоте x=w₀^.L и ЭДС, индуцируемую в статорной обмотке током возбуждения при синхронной частоте вращения:

E_q=w_c ^.M_d ^.i_r   .                                               (2.2.5)

Отличие частоты в переходном процессе от синхронной будем учитывать скольжением s ротора относительно синхронной оси по выражениям:

w=w_c^.(1+s),            s=(w-w_c)/w_c.

С учетом (2.2.5) и этих обозначений из (2.2.1-2.2.2) получим:

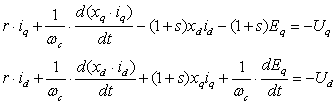                                 (2.2.6)

Известно, что значения потокосцеплений определяются через величины собственной и взаимных индуктивностей цепи:

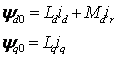                                                                             (2.2.7)

С учетом (2.2.5 и 2.2.7) Введем дополнительные  обозначения:

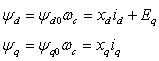                                                                                        (2.2.8)

Используя (2.2.8) можно получить окончательную, более компактную запись уравнений статорных обмоток:

1.    ;                                                   (2.2.9)

2.    .                                                  (2.2.10)

Аналогичным образом формируются уравнения роторных обмоток  (обмотки возбуждения, геометрическое расположение вектора тока в которой совпадает с продольной осью d, и короткозамкнутых демпферных обмоток, вектора токов в которых проецируются на обе оси). Заметим, что в уравнениях отсутствует вращающаяся составляющая, поскольку ротор (и его цепи) вращаются синхронно с осями q и d. Тогда уравнения 3, 4, 5 примут вид: