Сложная многосвязная электроэнергетическая система, страница 4

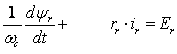3.   ;                                                            (2.2.11)

4. 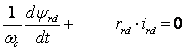  ;                                                          (2.2.12)

5. 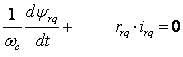   .                                                          (2.2.13)

Для того, чтобы система пяти уравнений движения была замкнутой, необходимо добавить уравнения механического движения ротора.

На рис.2.2.2 изображена система двух векторов  и .  Первый из них вращается с неизменной синхронной частотой ,  второй имеет частоту вращения ротора ω, которая, при возникновении переходных процессов отличается от синхронной. Т.е. величина электрического угла δ между векторами (рис.1.2) колеблется относительно некоторого установившегося значения в соответствии с соотношением (1.2.14), где величина s – упомянутое выше скольжение.

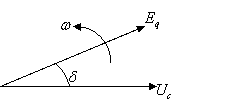
Рис. 1.2.2 – Векторная диаграмма электрического угла

                                                 (2.2.14)

Для полноты системы (равенства количества переменных и уравнений) необходимо включить в нее уравнение равновесия моментов:

   ,                                                                  (2.2.15)

в котором  -момент на валу турбины (постоянная величина, определяющая установившийся режим),  момент инерции, определяемый величиной скольжения и инерционной постоянной времени  :   .    - электромагнитный момент на валу генератора[ ]:

   .                                                                (2.2.16)

В этом случае уравнения движения ротора (6-7 по нумерации в соответствии с рис.2.2.1) примут следующий вид:

6.    ;                                                                              (2.2.17)

7.   .                                                        (2.2.18)

В окончательном виде систему уравнений движения (1-7), без учета мало влияющих на динамические свойства активных сопротивлений обмоток (r), можно переписать:

1. ;

2. ;

3. ;

4. ;                                                                       (2.2.19)

5. ;

6. ;

7. +.

Очевидно, что система уравнений движения (Горева-Парка) может быть структурно представлена в векторном виде:

.                                                                  (2.2.20)

Анализ структуры системы (2.2.19)) позволяет сделать вывод о том, что форма записи уравнений соответствует форме Коши (п.1.3). Это позволяет опираться на широко известные матричные методы анализа переходных процессов в многомерных системах.