Управление, сертификация и инноватика: Программа, методические указания и задания для контрольных работ и курсовой работы, страница 15

          Если 1 < m < 2,5, то прибор, неудобный ни для однократных измерений ни для многократных измерений.

          Для варианта 99, рассматривая манометр, как прибор предназначенный для однократного (обыкновенного), а не для многократного (статистического измерения, принимаем

2,5 ≤ m ≤ 3,5      или  .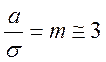

Если диапазон 0 – 400 кгс/см², а число делений n = 200, то цена деления – одно деление  2 кгс/см².

          Следовательно предельная погрешность отсчета 

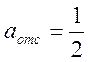 цена деления = 1 кгс/см²,

а следовательно СКО отсчета

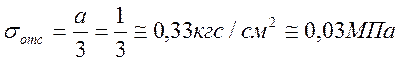
или 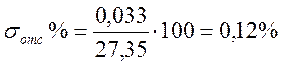 ,  а соответственно предельная погрешность  , δ_t% = 0,36%.

2. Предельная погрешность показания манометра вычисляется исходя из класса точности манометра ,

диапазон показаний  0 – 40 МПа,

отсчет по манометру Р_изб = 27,35 МПа,

Цена деления 0,1 МПа.

Аддитивная полоса погрешности 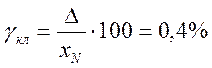 , где  - верхний предел манометра Р_пр = 40 МПа.

Абсолютная погрешность показания

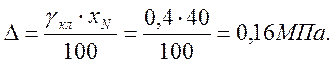
          Распределение погрешности показания манометра принимается равномерным;

          Относительная погрешность показания - СКО

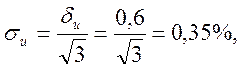
где      

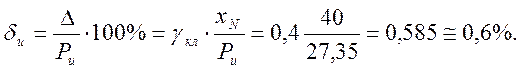
          3. Вариация показаний манометра, допущенного к применению не должна превышать абсолютного значения предела допускаемой основной погрешности показаний.

          Поскольку вариация манометра обуславливается гистерезисом трубчатой пружины, то закон распределения погрешности, из-за вариации можно принять антимодальное I (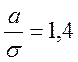) или антимодальное II (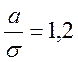) по ГОСТ 8.011-72.

Тогда принимая 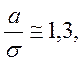 где  получим  .

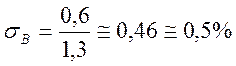4. В условиях  переменной температуры изменение модуля упругости трубчатой пружины приводит к появлению дополнительной температурной погрешности прибора.

          В соответствии с ГОСТ 2465-88 изменение показаний от воздействия температуры окружающего воздуха, выраженное в процентах диапазона показаний, не должно превышать значения, определяемого по формуле

Где К_t – температурный коэффициент не более 0,06%/^оС  для прибора класса точности 0,4; 0,6; 1 и 1,5 и не более 0,1%/^оС -= для приборов класса точности 2,5 и 4.

где  t₂ – действительное значение температуры в условиях эксплуатации,  t₁ = 20 или 23^оС с допускаемым отклонением:

          ± 2^оС для приборов класса точности 0,4; 0,6 и 1

          ± 5^оС для приборов класса точности 1,5; 2,5 и 4.

Для 99 варианта (класс точности 0,4) полагаем t₁ = 20 ± 2^оС.

          При изменении температуры t₂ в цехе от 10 до 30^оС, что составляет

Если не вводится соответствующая поправка, то температурная погрешность хотя бы должна быть учтена. Эта погрешность аддитивна, а распределение принимаем равномерным  ().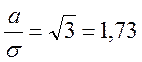

          Предельная погрешность

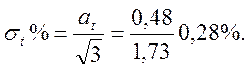
          5. Методическая погрешность измерения давления из-за неправильного выбора или выполнения места отбора давления составляет 0,2 – 0,35% измеряемого давления при скорости потока 15 – 20 м/с  и  0,4 – 0,7% при скорости потока 20 – 35 м/с.

          Ориентировочно принимаем

.

Если распределение этой погрешности близко к равномерному, то среднее квадратическое отклонение (СКО)

.

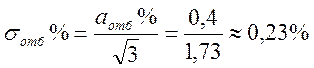          6. Если не вводится поправка на положение манометра относительно места отбора давления, то принимая Δh = ± 1 м

Тогда 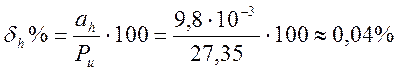  и принимая  распределение этой погрешности равномерным, находим СКО

,

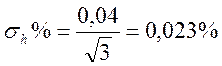Если разделительный сосуд не используется, то  .

Если же используется разделительный сосуд, то возникает дополнительная погрешность

          Полагая, что все частотные погрешности являются  между собой не коррелированны ( коэффициент корреляции ρ = 0) определяем результирующую СКО

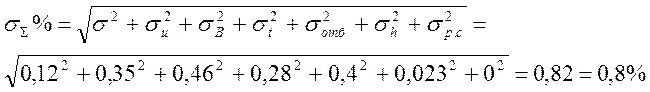
          В соответствии с предельной теоремой Чебышева, принимаем, что распределение результирующей погрешности распределено по нормальному закону Гаусса. Тогда доверительная погрешность результата при Р_D = 0,95

Или абсолютная доверительная погрешность результата измерения

.

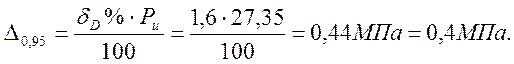Следовательно,

.

.

Эту результирующую погрешность можно оценить иначе.

Предполагаем, что все частные погрешности распределены равномерно. Тогда результирующая погрешность обыкновенного прямого измерения давления деформационным манометром

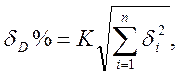
где  - предельные частные погрешности.

          Коэффициенты К приведены в таблице в зависимости от числа слагаемых m и доверительной вероятности  Р_D.