Управление, сертификация и инноватика: Программа, методические указания и задания для контрольных работ и курсовой работы, страница 12

Послед. цифра шифра	Действит. тем-ра поверхности tWoC	Температура окруж. среды tfoC	Предп. цифра шифра	Диаметр термоэлектродов d, мм	Материал	Теплопроводность объекта
0 1 2 3 4	145 140 135 130 125	15 20 25 30 35	0 1 2 3 4	0,11 0,12 0,13 0,14 0,15	Дерево сосна ┴ волокнам Дерево дуб ║ волокнам Дерево дуб ┴ волокнам Каменный уголь фарфор	0,15 0,63 0,21 0,19 1,04
5 6 7 8 9	120 115 110 105 100	40 35 30 25 20	5 6 7 8 9	0,16 0,17 0,18 0,19 0,20	Мрамор сталь мягкая сталь легированная алюминий медь	1,30 57 40 206 380

          Теплопроводность материала зависит от температуры. В таблице приведены ориентировочные значения 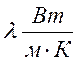 при температуре t_W.

Дополнительные сведения к задаче № 2

          Коэффициент теплоотдачи 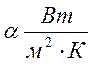 при рассмотрении конвективного теплообмена горизонтально расположенного круглого стержня (термопары) с окружающим воздухом вычисляется исходя из критериального уравнения в условиях свободной конвекции

,                        (1)

где  ,  .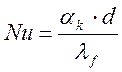

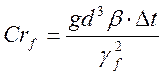Здесь   соответственно теплопроводность и кинематическая вязкость воздуха при температуре окружающей  среды t_f, коэффициент объемного расширения воздуха 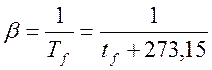 . Ускорение свободного падения g=9,8145 (для Новосибирска), g= 9,8155 (для Москвы).

В качестве примера приведены ниже вычисленные значения α_К в воздухе (принимая в первом приближении, что температура спая термопары t_сп t_W) для перегревов Δt=t_W-t_f = 5,50 и 500 град., d = 0,01; 0,1; 1 и 10 мм приведены в таблице 2.

Таблица 2

Перегрев Δt=tсп-tf≈ ≈ tW-tf	Определяющий размер  d мм
	0,01	0,1	1	10
5 50 500	1300 1400 2200	130 155 240	27 37 56	6,5 11,2 17,0

Как видно из приведенных данных в таблице коэффициент теплоотдачи  α_К в значительной степени зависит от определяющего размера d  и слабее от перегрева  Δt. Заметим в воде коэффициент  α_К, если d = 0,1 мм составляет 5200  и 8300 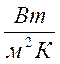 соответственно для перегревов 5  и  50 град.

Для варианта 99 вычисления по формуле 1, когда t_W, t_f = 20^oC, d = 0,2 мм  приводят к  α_К 106 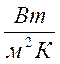, а линейный коэффициент лучистого теплообмена

,

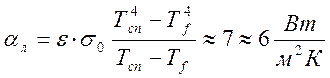где ε – степень черноты термоэлектрода, σ₀ – постоянная излучения Стефана-Больцмана.

Полный коэффициент конвективно-лучистого теплообмена

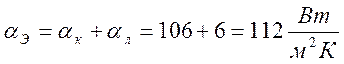
Для сокращения расчетов допускается принять во всех  вариантах

α_К=114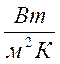,   α_л = 6 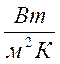  и следовательно  α_Э = 120 .

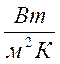Контактный термоприемник, например термопара, нарушает  первоначальное распределение температур в объекте, вследствие теплоотвода (теплоподвода) по нему. Поэтому измеренная температура t_изм = t_сп будет отличаться от действительной неискаженной температуры t_W.

          Эта методическая погрешность измерения  Δt_м = t_сп - t_ш  зависит от многих факторов: теплопроводности объекта λ₀  и термоэлектродов термопар (λ_Э d) характера теплообмена нагретой поверхности и термоприемника с окружающей средой, контактного термического сопротивления и т.д.

В случае идеального термического контакта термоприемника с поверхностью, методическая погрешность при его внешнем расположении можно вычислить, исходя из уравнения методической погрешности предложенной проф. Ярышевым Н.А.

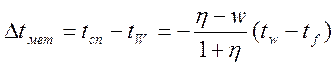                       (2)

где   ;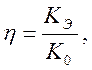

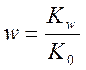Полная тепловая проводимость круглого стержня

K_Э = ,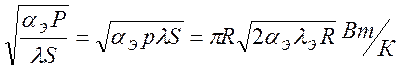   

где р – периметр, S – площадь сечения,  λ_Э – теплопроводность, α_Э – коэффициент теплоотдачи между термопарой и окружающей средой.

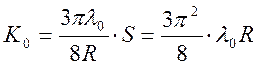 -  полная тепловая проводимость между глубинными слоями объекта и площадью контакта. Здесь λ₀ – теплопроводность объекта,  R – радиус контакта.