Работа и энергия. Преобразование кинетической энергии при переходе из одной инерциальной системы отсчета в другую

Лекция №5.

Работа и энергия.

В обыденном смысле работа понимается нами как, например, поднятие тяжестей. Представим себе штангиста, поднимающего груз на некоторую высоту. Чем больше груз, тем большая признательность зрителей и более почетное место в таблице достижений. Все пропорционально работе.

Введем определение работы. Будем называть - элементарной работой силы , совершенной на бесконечно малом пути  скалярное произведение . Согласно определению работа на конечном пути будет складываться из элементарных вкладов:

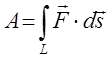                                         (1)

Можно показать, что работа инвариантна (лат. invariantis – неизменяющийся) относительно поворота системы координат. Инвариантность относительно поворота системы координат  - свойство любого скалярного произведения двух векторов. Относительно работы это свойство следует, в частности, из равенства угла между векторами   в произвольной декартовой системе координат. Напомним, что при неизменной силе -  .

Пример. Покажем свойство инвариантности в координатном представлении векторов.

Пусть ;  Работа . Повернем систему координат на угол против часовой стрелки. В повернутой системе координат:  По – прежнему:. Свойство инвариантности относительно поворота координатных осей доказано.

Определим мощность как работу, совершаемую за единицу времени:

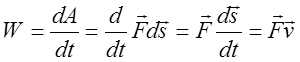                                 (2)

Единица измерения работы в системе СИ – 1 Джоуль. 1 Дж = 1 н 1м.

Единица измерения мощности  в системе СИ – 1 Ватт. 1Вт = 1 Дж / 1 c.

В системе CGS работа измеряется в эргах 1эрг = 1дн 1см = дж. Применяется также внесистемная единица измерения мощности – лошадиная сила (л.с.) 1л.с. = 736 Вт.

Связь работы с кинетической энергией.

            Допустим, что над телом совершается работа. Естественно предположить, что в этом случае меняется характер движения тела. В самом деле:

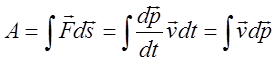, учитывая,  при  , тогда .

Утверждается, что . Опуская в дальнейшем знак модуля , получаем:

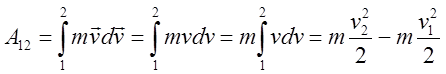                    (3)

Величину 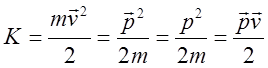 назовем кинетической энергией. Равенство (3) означает, что работа на заданном пути 1-2 равна приращению кинетической энергии.

                                       (4)

Пример. Проиллюстрируем «энергетический» подход к решению задач. Рассмотрим движение «доски» массы , длины на гладком столе. На доске расположен брусок массы . Между доской и бруском действует сила трения, коэффициент трения . Какую минимальную начальную скорость надо сообщить бруску, чтобы он дошел до противоположного конца доски?

Ясно, что эта задача вполне решается с помощью законов Ньютона. Решение уравнений движения позволяет получить скорости доски и бруска в произвольные моменты времени при различных начальных скоростях бруска.

Напишем закон сохранения импульса и рассчитаем изменение кинетической энергии тел системы. В горизонтальном направлении на систему брусок + доска силы не действуют ( сила трения является внутренней силой), проекция импульса сохраняется:

                                             (5)

В этом равенстве  соответственно скорости бруска и доски когда брусок находится на правом краю доски (см. рис.nn). Условием минимальности начальной скорости  - будет равенство конечных скоростей бруска и доски . Чуть большая скорость  приведет к соскальзыванию бруска с доски, чуть меньшая - не позволит достигнуть правого края. На брусок и доску действует внутренняя сила трения . Брусок она тормозит, доску ускоряет. Применим (5) к системе брусок + доска. Поскольку сила трения постоянна и ее работа совершается на длине доски, то:

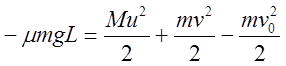                       (6)

Отрицательная работа силы трения потому, что сила и перемещение противоположны. 

После подстановки  (отметим, что эта скорость равна скорости центра инерции ) и несложных алгебраических преобразований находим:

.                               (7)

Рассмотрим разные предельные случаи (7). 1)  - масса бруска много меньше массы доски. . Минимальная скорость на почти покоящейся доске необходимая для прохождения пути очевидно равна . 2) Обратный предельный случай: . Масса доски существенно меньше массы бруска. . Легкая доска быстро разгоняется до скорости бруска, и тяжелому бруску трудно на пути L «обогнать» доску.

Преобразование кинетической энергии

при переходе из одной инерциальной системы отсчета в другую.

Работа силы и кинетическая энергия явно зависят от выбора системы отсчета. Рассмотрение этих величин в разных системах отсчета дает различные результаты. Например: человек давит с силой F на стенку вагона, движущегося равномерно в лабораторной системе отсчета (л.с.) со скоростью u. Работа в системе вагона нулевая , т.к. сдвига нет, а в л.с. работа отлична от нуля – .  Выходит, что зарплата работника зависит от выбора системы отсчета?  Обыденный опыт часто убеждает нас в справедливости этого.