Релятивистская динамика. Релятивистский импульс. Релятивистская энергия. Четырехмерный вектор энергии-импульса.

Лекция 12.

Релятивистская динамика.

Конечность скорости распространения сигналов, что другими словами скорости распространения взаимодействия существенным образом меняет классические законы динамики Ньютона. В релятивистской кинематике требуется учитывать запаздывание приложения сил.

Пример. Предположим, что в системе отсчета, в которой тела покоятся,  сила между ними действовала в течение некоторого времени, затем исчезла. В движущейся системе отсчета «выключение» взаимных сил действующих на разные тела произойдет в разные времена. НА основании такого простого умозрительного опыта можно утверждать, что третий закон Ньютона в релятивистской динамике несправедлив.

В действительности все силы в природе имеют локальный характер. Взаимодействие осуществляется через материального агента – поле. Поле, в частности электромагнитное, характеризуется измеримыми величинами – энергией, импульсом и др. В некоторых задачах, например задачах рассеяния частиц, можно пользоваться упрощенной моделью. Частицы до взаимодействия, находясь на бесконечно удаленном расстоянии друг от друга, не взаимодействуют. После рассеяния также будучи бесконечно удаленными частицы не взаимодействуют. Подобная модель будет применена для анализа сохранения импульса при столкновении частиц.

Релятивистский импульс.

            Классический закон сохранения в в виде:

несправедлив, т.к в нем отсутствуют ограничения на максимальную скорость частиц.

Будем предполагать, что в релятивистском случае импульс частицы также: , которое совпадает с классическим, за исключением того, что масса частицы может зависеть от скорости. Релятивистский импульс:

                                     (1)

где  при .  будем называть массой покоя частицы – эта та масса, которая измерена в сопутствующей частице системе отсчета. Таким образом постулируется, что релятивистский импульс является нелинейной функцией скорости.

Поставим мысленный эксперимент. Производятся выстрелы одинаковыми снарядами с одинаковыми в сопутствующих системах отсчета скоростями, перпендикулярно направлению движения поездов. В сопутствующих системах отсчета скорости снарядов равны  . Для простоты предполагаем, что скорости снарядов нерелятивистские . Считаем, что поезда движутся в направлении оси  неподвижной системы отсчета  со скоростями соответственно . Точное значение скоростей  каждого поезда несущественно, в дальнейшем следует задать относительную скорость одного поезда в системе другого равной (см. рис n1). Снаряды выстреливаются в направлении осей . Предположим, что в результате столкновения снаряды слипаются. Из соображений симметрии следует, что в неподвижной  системе отсчета   после столкновения импульс вновь образованного тела равен нулю. Если полный импульс вновь образованного тела в системе   нулевой, то в системе поезда 1, движущегося вправо поперечный импульс после столкновения и в силу сохранения и до столкновения также нулевой. Итак, в системе поезда 1, поскольку скорость  нерелятивистская, имеем:

.               (2)

Здесь  соответственно вертикальная и полная скорости снаряда, выпущенного из поезда 2 в системе поезда 1. Поскольку относительная скорость поезда 2 в системе поезда 1 равна  , то по закону преобразования поперечной скорости (см. лекц. 10 (12))  получаем:

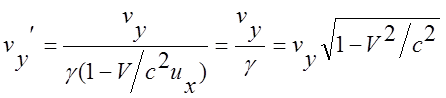                     (3)

Сравнивая (2), (3) находим:

                           (4)

Если устремить поперечные скорости снарядов  к нулю, то полная скорость , и , следовательно:

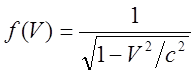                           (5)

Окончательно, релятивистский импульс выражается:

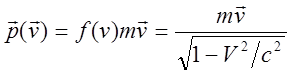                      (6)

Закон сохранения импульса в релятивистской динамике будет записываться в виде:

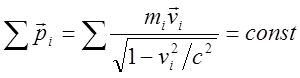                     (7)

Релятивистская энергия.

            Рассмотрим распад тела массы  на осколки масс .  В системе покоя  начального тела разлет осколков будет происходить в противоположные стороны. Пусть теперь тот же самый распад рассматривается с точки зрения системы отсчета  , движущейся с поперечной, относительно скоростей осколков  с нерелятивистской скоростью . Тогда, сохранение поперечной компоненты импульса, согласно (7) будет выглядеть следующим образом:

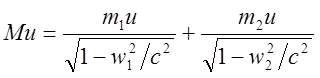                              (8)

В пределе, при  скорости осколков в сопутствующей системе  также будут устремляться к . После упрощения (8) имеем:

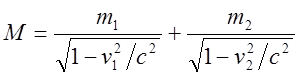                                 (9)

Согласно (9) масса начального тела больше суммы масс осколков! В более общем случае распада набора начальных масс  с образованием после распада набора продуктов   справедливо равенство:

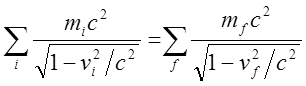                                (10)

Будем называть величину

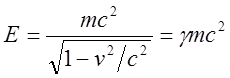                                             (11)

энергией частицы. Формула (11) применима в релятивистском случае. От нерелятивистского выражения кинетической энергии частицы формула (11) отличается на константу. Произведем разложение   по малости в пределе . Удерживая в разложении по степеням   два первых члена разложения: