Релятивистская динамика. Релятивистский импульс. Релятивистская энергия. Четырехмерный вектор энергии-импульса., страница 2

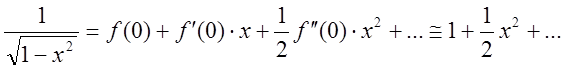
находим:

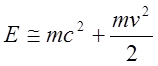.                                (12)

Видно, что при малых скоростях энергия представляет из себя сумму энергии покоя и нерелятивистской кинетической энергии. В общем случае кинетической энергией будем называть разность между полной энергией и энергией покоя:

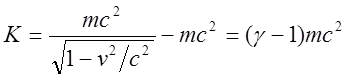                         (13)

            В физике высоких энергий, изучающей свойства элементарных частиц, принято использовать в качестве единицы измерения энергии 1 электронвольт –1 эВ.  1 эВ  – энергия, которую приобретает частица с зарядом, равным заряду электрона при прохождении разности потенциалов в 1 Вольт.

.

Помимо основной единицы 1эВ применяются также производные:

–  1 кило электронвольт = 1 КэВ = ,

–  1 мега электронвольт = 1 МэВ = ,

–  1 гига электронвольт = 1 ГэВ  = ,

–  1 тэра электронвольт = 1 ТэВ = .

Из таблицы видно, что энергия частицы по порядку величины составляющая 1ТэВ – (энергия протонного пучка на ускорителе  Тэватрон в Fermi National Acceleration Laboratory, близ Чикаго, USA)  приближается к 1 эргу!

Приведем также массы покоя некоторых элементарных частиц в енергетических единицах

Частица	Масса покоя,
Фотон
Электрон	0,511
мезон, нейтральный	140
Протон	938,3
Нейтрон	939,6
Промежуточный  бозон	91200

Четырехмерный вектор энергии - импульса.

           Введем 4-х вектор импульса по аналогии с 3-х мерным  импульсом заменив вектор скорости частицы  на 4-х мерную скорость (лекц. 11, (17)). Тогда :

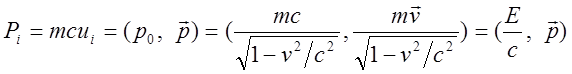                     (14)

Закон сохранения импульса следует записывать как закон сохранения 4-х мерного вектора:

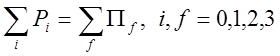                                               (15)

В выражении (15) можно выделить сохранение нулевой компоненты 4-х вектора, которая представляет собой закон сохранения релятивистской энергии и сохранение  суммы пространственных компонент – представляющего сохранение релятивистского 3-х импульса. В нерелятивистском пределе оба эти закона соответственно переходят в закон сохранения кинетической энергии и полного импульса системы.

           В релятивистской динамике энергия импульс являются компонентами одного 4-х вектора. Поскольку  - суть 4-х вектор, то он, очевидно, преобразуется при переходе из одной системы отсчета в другую согласно известным формулам:

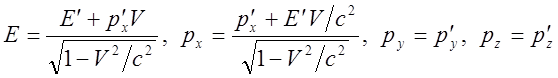                        (16)

Квадрат 4-х импульса является инвариантом относительно преобразований Лоренца:

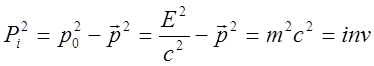                                           (17)

Из выражения (14) вытекает следующее соотношение между энергией, импульсом и скоростью свободной частицы:

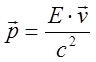                                                      (18)

Из (17) также следует:

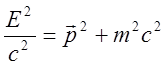                                           (19)

Найдем соотношение энергии с работой внешних сил. По определению, 3-х мерная сила равна скорости изменения 3-х мерного импульса (II-й закон Ньютона). Вычислим производную по времени от  . Дифференцируя левую часть находим:

, или:

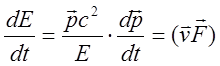                                 (20)

Так же как в классической механике: ,   . Изменение энергии равно работе сил.

Следствие. Получим 4-х вектор энергии – импульса для безмассовой частицы – фотона. . Согласно (19) получаем:

                                          (21)

Энергия фотона с частотой  равна . Составим 4-х вектор энергии – импульса фотона:

                                  (22)

Для волнового вектора модуль которого также существует 4-х вектор:

,                                   (23)

который преобразуется по формулам преобразования 4-х векторов. Отсюда, в частоности, следуют формулы преобразования частоты Допплера:

               (24)

Пример. Найти минимальные – «пороговые» энергии в лабораторной системе отсчета протонов необходимые для рождения антипротона в эксперименте на встречных пучках в реакции .

Пусть 4-х импульсы симметрично сталкивающихся протонов равны: . После столкновения в лабораторной системе образуется покоящаяся «составная» частица с массой равной как минимум 4-м массам протона.

Итак, 4-х импульс конечной составной частицы . В дальнейшем удобно пользоваться системой единиц, в которой . Записываем сохранение 4-х импульса в столкновении:

Возведем это равенство в квадрат для получения инвариантных слагаемых:

Подставляя в последнее  (напоминаем, что ) находим:

.

Следовательно: , отсюда: . Порог рождения антипротона в эксперименте на встречных пучках составляет две массы протона. Протоны следует ускорить до энергии большей 1,8 ГэВ.

           Для сравнения, нетрудно подсчитать пороговую энергию в той – реакции при столкновении протонов с неподвижной протонной мишенью. В этом случае