Лекция 11.
Релятивистская кинематика.
Аберрация.
Пусть в системе ![]() движется частица со скоростью
движется частица со скоростью ![]() под углом
под углом ![]() к оси
к оси ![]() . Определим, под каким углом
. Определим, под каким углом ![]() к оси
к оси ![]() движется
частица в системе отсчета
движется
частица в системе отсчета ![]() .
.
В системе отсчета ![]() проекции скоростей
частицы на оси
проекции скоростей
частицы на оси ![]() соответственно:
соответственно:
![]() . Применяя формулы преобразования
скоростей, имеем:
. Применяя формулы преобразования
скоростей, имеем:
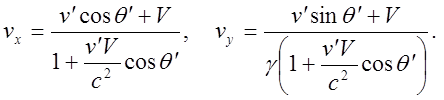 (1)
(1)
Откуда:
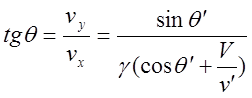 . (2)
. (2)
В предельном случае ![]() -
распространение светового фронта в обеих системах отсчета
-
распространение светового фронта в обеих системах отсчета ![]() происходит со скоростью
происходит со скоростью ![]() , находим:
, находим:
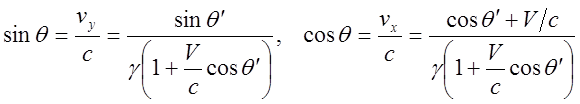 (3)
(3)
Формулы (3) описывают явление
световой аберрации. Преобразование угла ![]() как
функции
как
функции ![]() получается из (3) заменой
получается из (3) заменой ![]() . Выпишем полученные зависимости:
. Выпишем полученные зависимости:
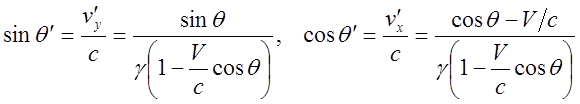 (4)
(4)
Исследуем полученные выражения.
На космическом корабле имеется «прожектор», излучающий свет, например, в
переднюю полусферу: ![]() . Согласно (3):
. Согласно (3):
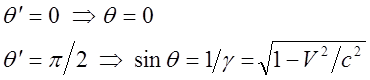
Если движение корабля происходит с ультрарелятивистскими
скоростями: ![]() , то
, то ![]() - свет,
излученный в переднюю полусферу в системе корабля соберется в узкий световой
конус
- свет,
излученный в переднюю полусферу в системе корабля соберется в узкий световой
конус ![]() в неподвижной системе отсчета
в неподвижной системе отсчета ![]() . Этот эффект называется эффектом «фары».
Отметим, что:
. Этот эффект называется эффектом «фары».
Отметим, что: ![]() - свет, излученный в заднюю
полусферу в системе отсчета
- свет, излученный в заднюю
полусферу в системе отсчета ![]()
![]() ,
распределяется за пределами узкого светового конуса с углом раствора
,
распределяется за пределами узкого светового конуса с углом раствора ![]() в системе отсчета
в системе отсчета ![]() .
.
Явление аберрации искажает картину звездного
неба, наблюдаемого в релятивистском космическом корабле. Согласно формулам (4)
с точки зрения космического наблюдателя свет от удаленных источников движется
со скоростью ![]() . Допустим, что в неподвижной системе
отсчета
. Допустим, что в неподвижной системе
отсчета ![]() свет от удаленного источника падает на
корабль под углом
свет от удаленного источника падает на
корабль под углом ![]() относительно направления
скорости корабля. В системе корабля -
относительно направления
скорости корабля. В системе корабля - ![]() угол,
под которым будет наблюдаться световой пучок:
угол,
под которым будет наблюдаться световой пучок:
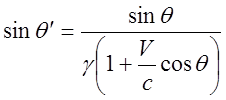 (5)
(5)
Если угол ![]() меняется в диапазоне от
меняется в диапазоне от
![]() до
до ![]() -
рассматривается передняя полусфера звездного неба, то
-
рассматривается передняя полусфера звездного неба, то ![]() .
Вся звездная полусфера будет рассматриваться наблюдателем в корабле в угле
.
Вся звездная полусфера будет рассматриваться наблюдателем в корабле в угле ![]() .
.
Впервые экспериментально
аберрацию света от удаленных звезд наблюдал Д. Бредли (1725). Он обнаружил, что
звезда ![]() Дракона, находящаяся практически в Земном
зените совершает сезонное движение с периодом в один год по круговой траектории
с диаметром 40,5 дуговых секунд. Согласно (4) при
Дракона, находящаяся практически в Земном
зените совершает сезонное движение с периодом в один год по круговой траектории
с диаметром 40,5 дуговых секунд. Согласно (4) при ![]() и
и ![]()
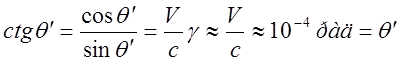 . Орбитальная скорость
Земли составляет
. Орбитальная скорость
Земли составляет ![]() . В дуговых секундах
. В дуговых секундах ![]() .
.
Аберрацию легко понять, применив аналогию между распространением света и падением дождевых капель. В отсутствии ветра дождевые капли падают на неподвижного человека вертикально, если человек движется, то дождевые капли падают под некоторым углом относительно вертикали.
Алгебра 4-х векторов.
Назовем четверку чисел расположенных в порядке ![]() 4-х вектором события. В 4-х векторе
4-х вектором события. В 4-х векторе ![]() принято называть 0-ю компоненту
принято называть 0-ю компоненту ![]() временной, а 1, 2, 3-ю компоненты
пространственными
временной, а 1, 2, 3-ю компоненты
пространственными ![]() . Ранее получены Лоренцевы
преобразования координат и времени при переходе из систем отсчета
. Ранее получены Лоренцевы
преобразования координат и времени при переходе из систем отсчета ![]() в
в ![]() и
обратные. Другими словами формулы преобразования определяют соотношения между
4-х векторами событий в различных системах отсчета. Удобно записать эти
преобразования в матричной форме. Считая любой 4-х вектор события вектором –
столбцом нетрудно представить линейное преобразование координат как
перемножение матрицы
и
обратные. Другими словами формулы преобразования определяют соотношения между
4-х векторами событий в различных системах отсчета. Удобно записать эти
преобразования в матричной форме. Считая любой 4-х вектор события вектором –
столбцом нетрудно представить линейное преобразование координат как
перемножение матрицы ![]() коэффициентов на вектор -
столбец события:
коэффициентов на вектор -
столбец события:
![]() .
.
Используя правила перемножения матриц имеем:
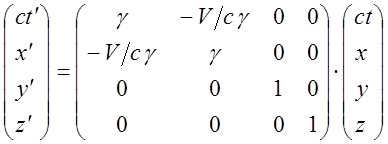 (6).
(6).
Здесь ![]() , всюду далее
обозначаем
, всюду далее
обозначаем ![]() . В матричной записи преобразований предполагается,
что
. В матричной записи преобразований предполагается,
что 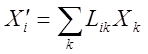 . Обычно знак суммирования по
повторяющемуся индексу опускают, предыдущая запись равносильно выглядит как:
. Обычно знак суммирования по
повторяющемуся индексу опускают, предыдущая запись равносильно выглядит как: ![]() . Обратное преобразование от компонент
4-х вектора события
. Обратное преобразование от компонент
4-х вектора события ![]() к компонентам
к компонентам ![]() , как нетрудно получить будет записываться
в форме:
, как нетрудно получить будет записываться
в форме: ![]() , где
, где ![]() элементы
обратной матрицы. Очевидно, что
элементы
обратной матрицы. Очевидно, что ![]() - дает единичную
матрицу, матрицу у которой на главной диагонали стоят 1. В матице обратного
преобразования произведена замена
- дает единичную
матрицу, матрицу у которой на главной диагонали стоят 1. В матице обратного
преобразования произведена замена ![]() . Окончательный вид
обратного преобразования имеет вид:
. Окончательный вид
обратного преобразования имеет вид:
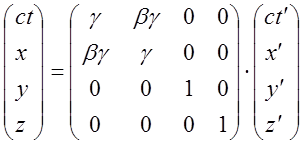 (7)
(7)
Непосредственным перемножением ![]() из (6)
на
из (6)
на ![]() из нетрудно убедиться, что
из нетрудно убедиться, что ![]() .
.
Любая четверка чисел ![]() преобразующихся
по закону (7) -преобразования компонент 4-х вектора события называется 4-х
вектором.
преобразующихся
по закону (7) -преобразования компонент 4-х вектора события называется 4-х
вектором.
Введенный подобным образом объект –4-х вектор подчиняется правилам векторной алгебры.
Сложение 2-х 4-х векторов выполняется по правилу: если ![]() - 4-х вектора, то
- 4-х вектора, то ![]() .
.
Определим скалярное произведение 4-х векторов следующим
правилом. Пусть ![]() . Назовем скалярным произведением
величину:
. Назовем скалярным произведением
величину:
![]() (8)
(8)
Наиболее важным свойством
скалярного произведения векторов является его инвариантность. Инвариантность
(от лат. invariantis – неизменяющийся) означает
сохранение величины скалярного произведения в различных системах отсчета. В
релятивистской кинематике следует убедиться в неизменности скалярного
произведения в случае Лоренцева преобразования компонент векторов. Прямой
подстановкой компонент ![]() , выраженных через
, выраженных через ![]() согласно формулам (7) нетрудно убедиться,
что:
согласно формулам (7) нетрудно убедиться,
что:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.