Разложение плоского движения твердого тела на поступательное и вращательное
Любое движение твердого тела, в том числе движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых поступательное (переносное), а другое – вращательное (относительное).
|
|
Пусть тело в своем движении переходит из одного состояния в другое. Мы можем представить это движение двумя способами: 1) тело совершает поступательное перемещение, когда точка А совмещается с А1, потом доворачиваем тело вокруг точки А1, 2) тело совершает поступательное перемещение, когда точка В совмещается с В1, потом доворачиваем тело вокруг точки В1, Точки А1 и В1, вокруг которых мы доворачиваем фигуру, называют полюсами. Нетрудно заметить, что поворот фигуры всегда будет одним и тем же (на угол j), независимо от выбора полюса. Поступательное перемещение зависит от выбора точки – полюса. |
§ 2.12. Скорость точек тела при плоском движении. Мгновенный центр скоростей.
|
|
Выбираем точку А за полюс – начало отсчета подвижной системы координат, движущейся только поступательно, относительное движение будет "чистым" вращением. Параллельность осей: Аx' || Ox ; Ay' || Oy Из
уравнений для сложного движения точки
|
Скорость какой-либо точки фигуры при ее плоском движении равна векторной сумме скорости полюса (переносной) и относительной скорости этой точки от вращения фигуры вокруг полюса. Эта формула выражает зависимость между скоростями двух любых точек тела при плоском движении в любой момент времени.
В каждый момент времени при плоском движении фигуры, если w¹0, имеется единственная точка этой фигуры (или ее продолжения), скорость которой равна нулю. Эту точку называют мгновенным центром скоростей. Обозначим ее Р.
|
|
Необходимо указать способ нахождения полюса. Пусть есть плоская фигура, нам известна скорость движения ее полюса О' и угловая скорость вращения вокруг полюса - w. Скорость точки Р равна нулю, если |
Мгновенный центр скоростей является единственной точкой плоской фигуры для данного момента времени. В другой момент времени в общем случае мгновенным центром является уже другая точка плоской фигуры.
Если мгновенный центр скоростей известен, то скорости точек плоской фигуры при ее движении в своей плоскости вычисляют также, как и в случае вращения фигуры в рассматриваемый момент времени вокруг своего мгновенного центра скоростей с угловой скоростью w.
Способы нахождения мгновенного центра скоростей.
Мгновенный центр скоростей можно найти либо из механических условий задачи (точка касания колеса, катящегося без проскальзывания), либо по скоростям точек плоской фигуры.
|
|
Если известны скорости двух точек плоской фигуры, мгновенный центр скоростей находится на пересечении перпендикуляров к скоростям этих точек |
||
|
В том случае, когда точки лежат на общем перпендикуляре к скоростям этих точек и скорости точек параллельны, концы векторов скоростей точек лежат на одной прямой, проведенной через мгновенный центр скоростей, так как скорости точек пропорциональны расстояниям от этих точек до центра скоростей. |
|
||
|
|
Если скорости двух точек, расположенных на общем перпендикуляре к этим скоростям, еще и равны, мгновенный центр скоростей находится на бесконечности и мы имеем мгновенное поступательное движение плоской фигуры, при котором скорости всех точек фигуры одинаковы по модулю и направлению, w=0. При этом мгновенном поступательном движении только скорости точек одинаковы, а их ускорения в общем случае различны. |
||
|
Невозможен случай, когда скорости двух точек, не лежащих на общем перпендикуляре к скоростям, не равны друг другу по модулю, но параллельны, так как для него не выполняется теорема о проекциях скоростей на прямую, соединяющую эти точки. |
|
||
|
|
Пример. У колеса, катящегося по горизонтальной плоскости без проскальзывания со скоростью v0, мгновенным центром скоростей является точка контакта колеса с плоскостью.
|
Вычисление угловой скорости при плоском движении.
Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно определению, как
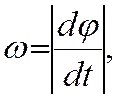
Также ее можно определить так:
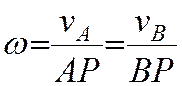
Величину w можно
вычислить путем предварительного нахождения скорости какой-либо точки плоской
фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс: 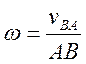 , знак угловой скорости определяют по направлению
относительной скорости.
, знак угловой скорости определяют по направлению
относительной скорости.
Еще один способ такой: если предварительно установить зависимость угла поворота плоской фигуры от линейных угловых величин других плоских фигур тождественным соотношением, то дифференцируя его по времени, получаем соотношение, из которого иногда удается определить искомую угловую скорость.
|
|
Пример. В несимметричном (смещенном) кривошипно-шатунном механизме установить зависимость между угловыми скоростями кривошипа OA - w и шатуна AB - w1: Для j<p/2 r Sinj + h = l Siny После
дифференцирования Учитывая,
что (при h=0 и r=l w = w1) |
§ 2.13. Ускорения точек при плоском движении. Мгновенный центр ускорений.
За переносное движение тела примем поступательное движение, за относительное движение – вращение тела вокруг полюса А.
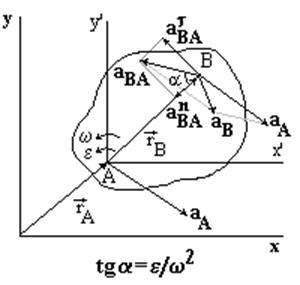 Полюс
А движется с ускорением aA и тело вращается вокруг полюса с угловой скоростью w и угловым ускорением e. Из формул для сложного движения
точки имеем:
Полюс
А движется с ускорением aA и тело вращается вокруг полюса с угловой скоростью w и угловым ускорением e. Из формул для сложного движения
точки имеем:
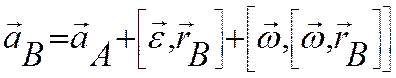
Эту формулу можно представить в виде:
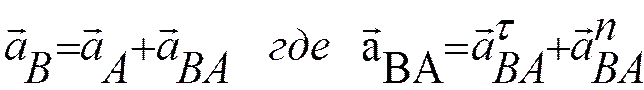
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.