Работа и энергия. Преобразование кинетической энергии при переходе из одной инерциальной системы отсчета в другую, страница 3

Здесь единичные орты в направлении осей. Значок  «набла» (набла - древнееврейский музыкальный инструмент) – означает процедуру вычисления производных.  На принятом в современной литературе языке - оператор. Говорят, что  - «градиент»

Пример. Найдем градиент ньютоновского поля тяготения. 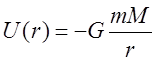, Последовательно вычисляя частные производные имеем:

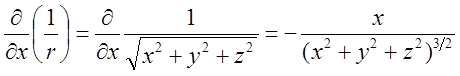. Убеждаемся, что .

Полная сила, как и следовало ожидать:

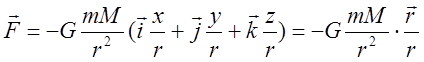                        (17)

Получен закон всемирного тяготения.

Закон сохранения энергии.

Ранее рассмотрены случаи перехода работы в кинетическую, либо потенциальную энергии. В общем случае работа внешних сил приводит к изменению и кинетической и потенциальной энергий. Из (10) следует: . Учитывая, что получаем:

                                        (18)

Работа внешней силы равна сумме изменений кинетической и потенциальной энергий.

Будем называть сумму потенциальной и кинетической энергий – полной. Тогда:                                         (19)

Пример. Внешняя сила действует вертикально вверх в однородном поле тяжести с ускорением свободного падения . На высоте  скорость тела . Соотношение (19) связывающее на высоте требует:

.

Если , то , в противном случае .

Рассмотрим замкнутую систему, взаимодействие с внешними телами исключено, . В этом случае, поскольку , то . Другими словами сумма . Следовательно :

                                               (20)

Полная энергия замкнутой системы сохраняется. Это выражение фундаментального закона сохранения энергии.

Пример. Происходит распад составного тела под действие первоначально сжатой пружины. Пусть массы тел после распада соответственно . Максимальная деформация пружины -. Внешних сил нет. Импульс и полная энергия системы сохраняется.

,

.

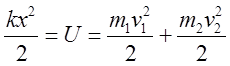Скорости - скорости тел после распада. После несложных преобразований:

.

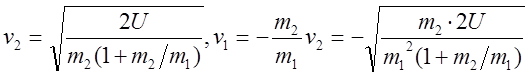Всегда, как только получено решение задачи, требуется его проанализировать.

Априори ясно, что при одинаковых массах скорости тел должны быть одинаковы. В самом деле, подстановка в выражения для скоростей дает одинаковые значения 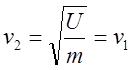. Если одна из масс существенно больше другой, например  , то 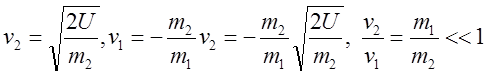. Чем массивнее частица, тем меньше ее конечная скорость.

Функция Гамильтона.

Потенциальная энергия механической системы в общем случае зависит от обобщенных координат. . Будем считать, что кинетическая энергия системы есть функция обобщенных импульсов. . Составим характеристическую функцию:

                                        (18)

Функция  называется функцией Гамильтона, или Гамильтонианом.

Введение характеристической функции Гамильтона позволяет выписать замечатоельно симметричные обыкновенные дифференциальные уравнения – уравнения Гамильтона, являющиеся аналогами уравнений движения. Приведем без доказательства вид уравнений Гамильтона.

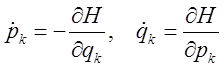                                        (19)

Пример. Одномерный механический осциллятор – грузик на пружинке описывается функцией Гамильтона:

.

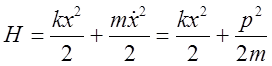Вычисление производных дает:

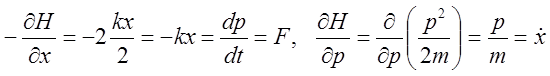
Устойчивость механических систем.

      Рассмотрим систему взаимодействующих материальных точек в отсутствие связей. Будем считать все действующие между частицами силы консервативными, в этом случае:

,

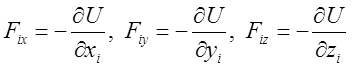здесь - координаты - частицы, - компоненты, действующей на частицу силы. Система находится в равновесии, если , или . Для равновесия необходимо, чтобы потенциальная энергия была стационарна, т.е при любом малом смещении частиц из состояния равновесия приращение потенциальной энергии будет величиной более высокого порядка малости по сравнению со смещением. Следовательно, требуется, чтобы потенциальная энергия имела экстремум – максимум, либо минимум. Утверждается, если потенциальная энергия имеет минимум, то положение равновесия устойчиво – малое смещение из положения равновесия вызывает появление возвращающих в него сил. Действительно: (см. рис. 3) - значение потенциальной энергии в минимуме. Пусть произошло смещение из положения равновесия при этом  и - значение потенциальной энергии в смещенном положении. . Из закона сохранения энергии , следовательно , поскольку кинетическая энергия не может быть отрицательной. Ограниченность потенциальной энергии означает ограниченность области пространства, в которой совершается движение. Говорят, что система совершает финитное (ограниченное) движение. А это и есть устойчивость положения равновесия. Нетрудно убедиться, что вблизи положения равновесия разложение потенциальной энергии по координате в простейшем одномерном случае должно начинаться со слагаемых квадратичных по координате:

Из условия 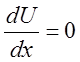 следует: