В растворах слабых электролитов, которые диссоциированы лишь отчасти, справедливо уравнение Аррениуса, которое связывает l и l0 со степенью диссоциации a:
. (5)
Если учесть в уравнении Аррениуса межионные взаимодействия, то для 1,1-валентного электролита оно приобретает вид
. (6)
Электропроводность электролитов связана со скоростями движения ионов в растворе. Скорость движения Vi [м × с–1] иона в растворе пропорциональна напряженности приложенного электри-ческого поля E [В × м–1]:
Vi = Wi × E.
Коэффициент пропорциональности Wi [м2× с–1× В–1] называется подвижностью иона. Ионная электропроводность пропорциональна подвижности иона. При степени диссоциации α = 1 коэффициентом пропорциональности является число Фарадея (96 500 K / г-экв)
и 
.
Доля тока, переносимая данным ионом, называется числом переноса ti иона:
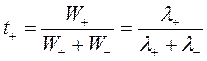и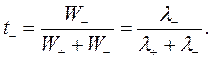 
В соответствии с законом Стокса при движении в
жидкости шарообразной частицы радиусом 
под
действием силы 
, скорость её движения 
следующим образом зависит от вязкости 
.
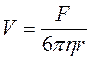Применение закона Стокса к кондуктометрии дает уравнение, связывающее подвижность иона, его заряд и радиус
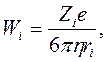
где
– заряд электрона.
Теория Дебая–Хюккеля позволяет рассчитывать коэффициенты активности ионов. Для наглядности представим себе большой многозарядный ион, например, положительно заряженную коллоидную частицу, которая помещается в раствор электролита. Вблизи этой частицы происходит перераспределение ионов, возникает избыток анионов и недостаток катионов в сравнении со средней по раствору концентрацией. Если зафиксировать это распределение, или ионную атмосферу, и убрать из раствора коллоидную частицу, то в месте, где она располагалась, обнаружится потенциал, создаваемый ионной атмосферой. Ясно, что если вернуть частицу обратно в раствор, то её энергия будет зависеть от потенциала ионной атмосферы в точке, где она находится. Задача теории состоит в определении коэффициента активности заряженной частицы, зависящего от энергии её взаимодействия с ионной атмосферой. Выводы теории оказываются справедливыми и для частиц небольшого размера, включая однозарядные ионы. Важным параметром теории является радиус ионной атмосферы ra, который рассчитывается по формуле
,
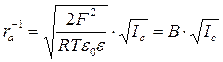где
для воды при 25 0 С. При ионной силе раствора равной, например, 10–2 М, радиус ионной атмосферы » 3 нм.
Итак, каждый ион в растворе окружен симметричной ионной атмосферой, образованной ионами противоположного знака. Наличие ионной атмосферы ведёт к снижению скорости движения иона. Действуя на ион, поле одновременно действует и на его атмосферу, заставляя её сдвигаться в противоположном направлении. В результате возникает тормозящий эффект, который получил название электрофоретического. Кроме того, при движении иона нарушается сферическая симметрия его ионной атмосферы и появляется сила кулоновского взаимодействия, направленная противоположно внешнему полю. Этот эффект тем больше, чем больше скорость иона, и приводит к дополнительному торможению, пропорциональному скорости. Второй эффект называется релаксационным.
Применение теории Дебая–Хюккеля к задаче измерения электропроводности растворов электролитов приводит к формуле (6). Проверим размерность величины В, а также коэффициентов b1и b2:
,
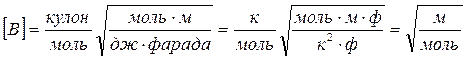или, если ионная сила измеряется в моль/л, для размерности В имеем
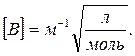
Учтено, что
, 
.
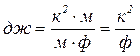Размерность величины (b1×Ic1/2) совпадает с размерностью эквивалентной электропроводности l:
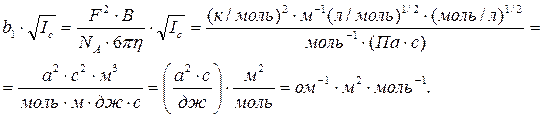
Произведение b2×Ic1/2 является безразмерной величиной
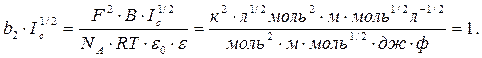
Поэтому размерность b1есть
,
а размерность b2:
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.