Первая и вторая теоремы Вейерштрасса. Теория локального экстремума. Аксиомы вещественных чисел

1 и 2 теоремы Вейерштрасса

Первая теорема Вейерштрасса : Всякая непрерывная функция , заданная на отрезке , ограничена, т.е. числа m и M такие, что  .

Доказательства: Докажем ограниченность сверху, т.к. снизу аналогично!!!

1) -ограничена сверху, - это надо доказать. Предположим, что это неверно.

2) т.е. , такое что

3) Возьмем , что

4) Меняем получаем последовательность . Выделяем сходящуюся подпоследовательность:

5) т.к. - непрерывная

6) Если в 3) взять n=1 ,  но , противоречие => 2) – не верно т.к. верно1) => теорема доказана для M, а для m – аналогично

Вторая теорема Вейерштрасса: Всякая непрерывная функция, достигает своих наибольшего и наименьшего значений, т.е. если 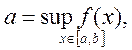 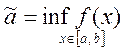, то и , что  а

Доказательство: Только для sup, т.к. inf аналогично. Надо доказать, что, такие что  где . Допустим, такой точки нет, т.е. . Рассмотрим 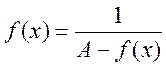,  для  по построению и - непрерывна, т.к. 1-непрерывна и разность тоже => -непрерывна => по 1-ой теореме Вейерштрасса она ограничена сверху, т.е. А₁>0, что  , подставим вместо   

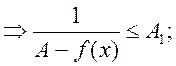
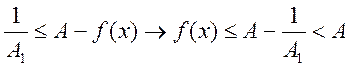
Аксиомы вещественных чисел:

Аксиомы  чисел. R – это произвольное множество, в котором определены операции,  операции сравнения

Аксиомы поля:

1.

2.

3. что

4. , что

5.

6.

7.  что

8. что

9.

Упорядоченное поле:

1. Из

2. Если

3.  либо , либо

4. если

5.

Архимедово поле

 целое

Аксиома непрерывности:  - вложенные отрезки,  и . 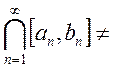Æ - это значит, что на прямой нет дырок

Выпуклые функции: веществ. функция , B – выпуклое множество, называется выпуклой, если выполняется неравенство:  для где 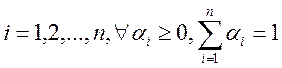. Если n=2 , то будем рассм. формулу Иенсена.

Интегрирование по частям

Теорема: пусть функции  и - непрер. диф-мые на выполняется

Доказательство: 1) - по определению, ; 2) ; 3) ; 4)  ; 5)

γ- и β-функции.

Определение: Эйлеров интеграл первого рода. Так называется ( по предложению Лежандра) интеграл вида:

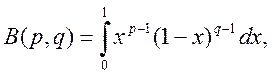 где p, q>0.

Он представляет функцию от двух переменных параметров p и q: функцию B(«Бета»).

Определение: Эйлеров интеграл второго рода. Это название было присвоено Лежандром замечательному интегралу:

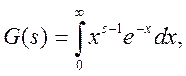
Который сходится при любом s>0 и определяет функцию G («Гамма»).

Докажем, что: 1. G(s+1)=s*G(s);

                         2.

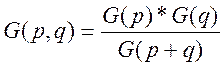
G(1)=1; G(2)=G(1)=1; G(3)=2*G(1)=2!;…; G(n+1)=n!, nN, то есть G-это аналог факториала, а B- аналог биномиального коэффициента.

Доказательство:

1.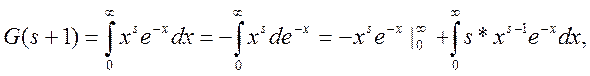 где в пределе

2. Рассмотрим

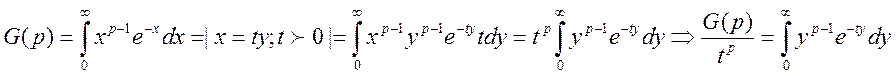
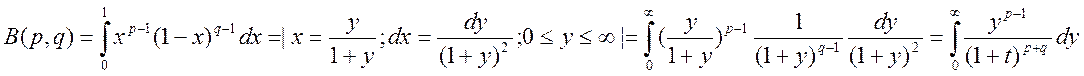
Составим 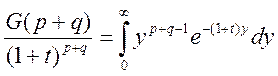 и проинтегрируем по t

Левую: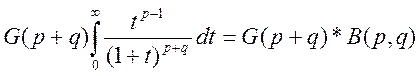

Правую: 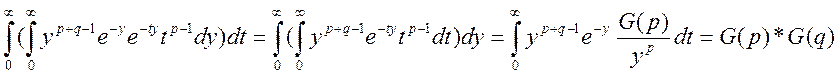, все доказано, так как G(p+q)*B(p,q)=G(p)*G(q)

Классы интегрируемых функций.

Теорема 1:.Если функция f(x) – непрерывна на отрезке [a,b], то она интегрируема на [a,b].

Доказательство:Составим разность: S_n-S_ǹ = (M_k  - m_k )∆x_k = (f(ξ_k) - f(ξ ̀_k)) ∆x_k

Т.к. функция f(x) – непрерывна на [a,b] => f(x) – непрерывна на [x_k-1,x_k] => $ ξ̀_k и ξ ̀_k Î [x_k-1,x_k], что M_k = f(ξ_k), m_{k =} f(ξ ̀_k)  Т.к. f(x) непрерывна на [a,b] =>  равномерно непрерывна на [a,b] => для  e >0 $ d, что ½x - x'½< d => ½ f(x) - f(x')½< e Возьмём разбиение мелкости l_n< d => ½(f(ξ_k) - f(ξ ̀_k)) ∆x_k ½£ e×∆x_k  = e×(b-a)®0 теорема  доказана!!!

Теорема 2: Монотонная, ограниченная функция f(x) на отрезке [a,b], интегрируема.

Доказательство: Монотонная => x £ x' => f(x) £ или ³ f(x') Пусть f(x) – монотонно неубывающая  функция =>  êS_n- S_n ̀ê=(M_k  - m_k )∆x_k , M_k = f(x_k), m_{k =} f(x_k-1) => 

êS_n- S_n ̀ê=( f(x_k) - f(x_k-1))∆x_k£ êêпусть мелкость разбиения l_n< e => ∆x_k £ l_n £ e êê£ e×( f(x_k) - f(x_k-1))∆x_k = e×(f(b)-f(a)), а т.к. e - произвольное => êS_n- S_n ̀ê0, при l_n ® 0, Ч.Т.Д.

Критерий Коши – существование предела: для того чтобы имела конечный предел при , необходимо и достаточно, чтобы для , что для всех  и  и таких, что . Доказывается сведением к последовательности.

Критерий Коши:для того чтобы последовательность  сходилась, необходимо и достаточно, чтобы она была фундаментальной.

Доказательство:  Необходимость. если 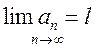, то для любого  существует , такое, что для всякого  имеем .

Следовательно, для любых  

.

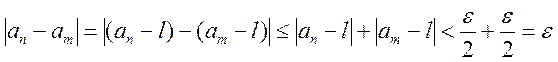Поэтому  - фундаментальная последовательность.

Достаточность. По условию последовательность  является фундаментальной.

1. Докажем, что  ограничена. В самом деле, возьмем =1. Тогда найдется n₀=n₀(1) такое, что для всех  имеем . Но тогда  . Отсюда .

2.  В силу теоремы Больцано-Вейерштрасса существует сходящаяся подпоследовательность  при . Условие её сходимости можно записать так:   такое что  имеем . Пусть  и . Тогда  для всех n>N и n_k>N имеем 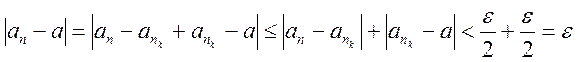 , т.е. последовательность  сходится.