Первая и вторая теоремы Вейерштрасса. Теория локального экстремума. Аксиомы вещественных чисел, страница 3

Теперь докажем, что  сходится. Для этого заметим, что длина отрезка  равна , откуда при . Это значит, что последовательность вложенных отрезков  стягивается и все отрезки  имеют единственную общую точку . Именно это число  и будет пределом для . Действительно, если  то . Но так как при , то и , откуда . И так как , то  при , что и требовалось доказать.

Теорема Вейерштрасса о равномерном приближении  непрерывной функции полинома

Теорема: полином 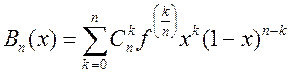 равномерно сходится к непрерывной функции F(x) xÎ[0;1].

Вспомогательная лемма: имеют место соотношения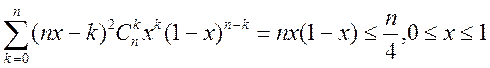

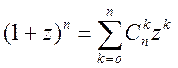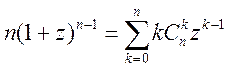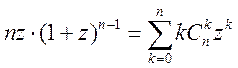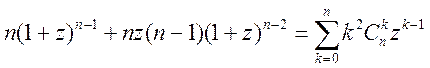Доказательство: рассмотрим  (1) , продифференцируем по z   , умножим на z, (2) , продифференцируем по z , умножим на z,  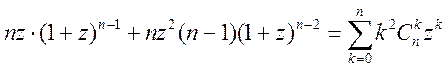, (3) 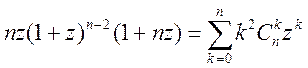.  Пусть 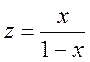, где 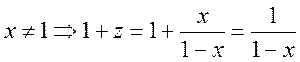 подст. в (1) , переносим т.е. 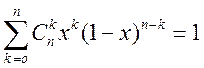 - это (4). Подстав. во (2) 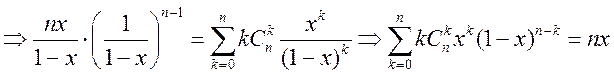 - это (5). Теперь подставим z в (3) 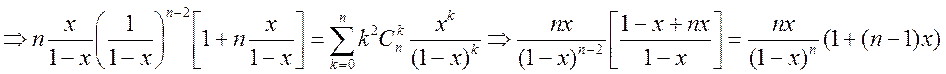Прив. к общ. зн. 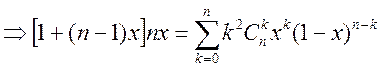- это (6). (4) умножим на , (5) – на , а (6) – на 1  всё склад. 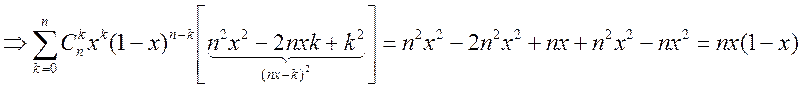. Лемма доказана.

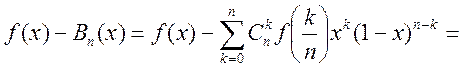
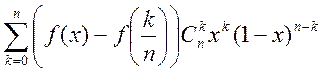
Доказательство теоремы: рассм. разность  ; по (4) в лемме. (по 1-ой теореме Вейерштрасса), по теореме Кантора

 ;

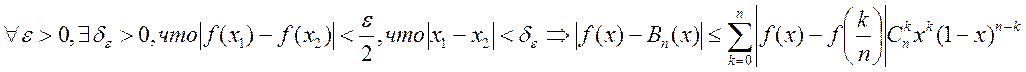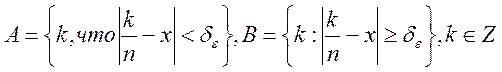, наша

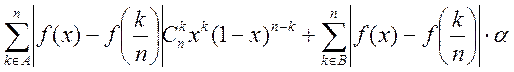
1) оценим 1-ую сумму: 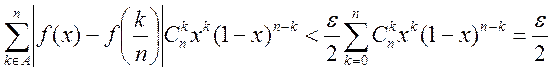, т.к.  по (4) в лемме. 2) оценим 2-ую сумму: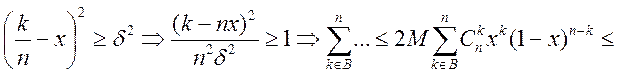

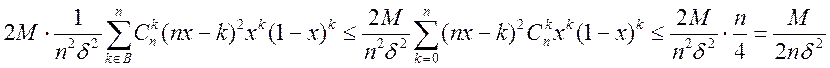, т.е. 2-ая сумма ограничена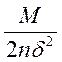 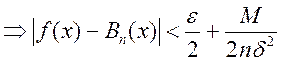, Пусть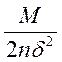 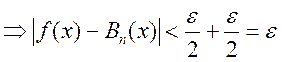. Ч.т.д.

Теорема Кантора

Теорема: всякая непрерывная функция, заданная на компакте  , равномерно непрерывна.

Доказательство: надо доказать, что равномерна, непрерывна. Докажем от противного . Пусть 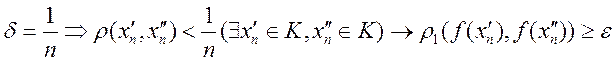. Выделяем  и из второй (причем номера  совпадает с номером первой послед.). Докажем, что : рассм. (по нер-ву ) .

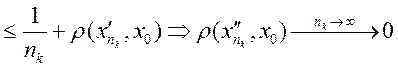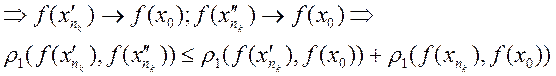
Но если подставить  противоречие.

Теорема о неподвижной точке

Теорема:  всякое сжимающее отображение  полного метрического пространства М в себя имеет неподвижную точку, и притом только одну.

Доказательство: (методом послед. приближений) (- произвольная точка) и строится

. Докажем - неподвижная точка: (т.к. сжат.) т.е. , где k- любой. Рассм. (т.е. добавили точку  и воспользовались неравенством )(воспольз. оценкой) 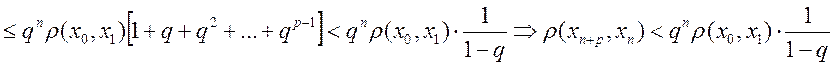 (получим оценку) 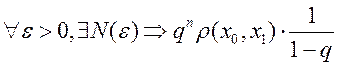, что - последовательность фундаментальна, а т.к. пр-во полное . Теперь док-ем, что x-неподвижная точка. Рассм. расст. при , , точка неподвижна. Докажем, что она единственна: и  противоречие. Теорема доказана.

Теорема о пределе монотонной последовательности

Теорема: всякая МВП и ограниченная сверху, имеет конечный предел и всякая МУП и ограниченная снизу, имеет конечный предел.

Доказательство: рассм.  - монотонно возр., Е огр. сверху по теореме о верхней грани , - и есть предел . 1)  2) что , , т.к. посл. монот. растет

Теорема Ролля:

Теорема: Пусть выполнены условия: 1) функция  имеет конечную производную на  (открытый промежуток) 2)  - непрерывна на  3)  тогда  внутренняя точка  

Доказательство:

- непрерывна на (2) на этом отрезке найдется точка , которой  имеет , а также точка , являющейся точкой  для . Если , то постоянна на отрезке  и  всюду на . И та точка из них, для которой равенство не имеет места, будет внутренней точкой отрезка  и одновременно точкой локального экстремума. Обозначив ее через , имеем , поскольку в противном случае была бы точкой возрастания или точкой убывания функции .

Теорема Лагранжа

Теорема: (теорема о конечных приращениях):

Пусть функция , , непрерывна на отрезке , имеет  конечную производную на . Тогда  внутренняя точка с, , что 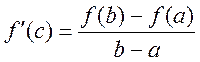. Это геометрический смысл -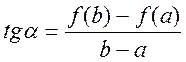

Доказательство: Рассмотрим 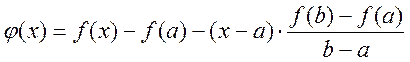,  =>, - непрерывна на отрезке , дифференцируема на  и (=> удовлетворяет условие теоремы Ролля) => , что ,

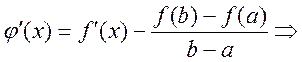
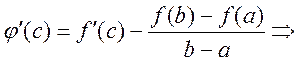
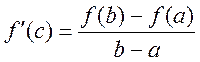
Теорема Коши:

Теорема: Пусть функция  и ,  непрерывны на отрезке  и имеют конечные производные  на , причем  либо >0, либо <0, т.е. >0, либо <0. Тогда  внутренняя точка с, , что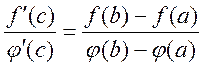

Доказательство: Рассмотрим функцию 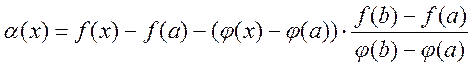, , если подставим => удовлетворяет теорему Ролля => c, что .

Теорема Тихонова

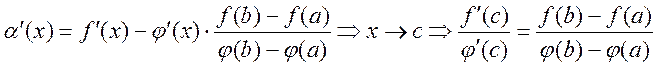
Теорема: пусть - непрерывная функция. И выполнены условия: 1) функция  имеет обратную . Обратная – единственная. 2) метрическое пространство  является компактом. Тогда обратная функция  непрерывна на .

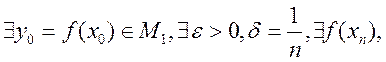Доказательство: - надо доказать, что непрерывна  1)  и  ; 2) Надо док-ть противное,    - отрицание ; 3) пусть ; 4)  что 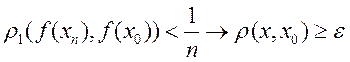- неравенство*. Выделим сход. подпослед.  т.к. . Докажем, что  по непрерывности подставим в неравенство*: 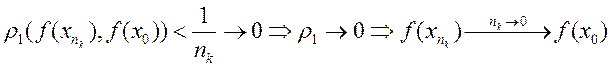.В силу единственности предела , а т.к. существует обратная единственная функция . Тогда  - мы доказали. Но из неравенства* - то эти 2 соотнош. против.