Операции множеств: а) объединение 2-х множеств - ![]() - это множество, которое состоит из
элементов и E1, и E2.
- это множество, которое состоит из
элементов и E1, и E2.
б) пересечение двух множеств - ![]() - это
множество всех общих элементов множеств E1 и
E2.
- это
множество всех общих элементов множеств E1 и
E2.
в) дополнение – сE – если ![]()
Непрерывные функции:
функция ![]() , называется
непрерывной на Е, если она непрерывна в каждой точке множества Е
, называется
непрерывной на Е, если она непрерывна в каждой точке множества Е
Неравенство Иенсена.
![]()
Теорема: Пусть функция ![]() выпукла
вниз, тогда имеет место неравенство
выпукла
вниз, тогда имеет место неравенство
![]() Доказательство (методом мат.
индукции):
Доказательство (методом мат.
индукции):
1) n=2 – верно 2) n=k – верно 3) докажем для (k+1).
Рассмотрим ![]() , где
, где ![]() и
и 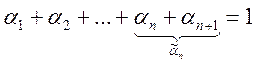 . Если
одно из
. Если
одно из ![]() верно для n=k
верно для n=k ![]() будем
считать, что
будем
считать, что ![]() . Тогда
. Тогда 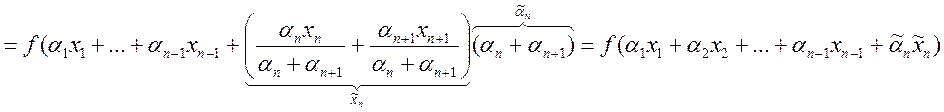 -
верно по индукции
-
верно по индукции ![]()
![]() .
.
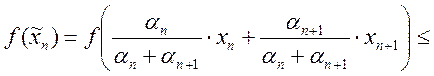 (во условию выпуклости)
(во условию выпуклости) 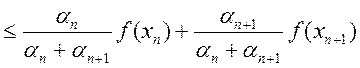 и подставим большую величину
и подставим большую величину ![]()
Несобственные интегралы. Критерий их сходимости.
Определение: 1) пусть функция ![]() определена
на
определена
на ![]() и интегрируема на
и интегрируема на ![]() .
Тогда предел при
.
Тогда предел при ![]()
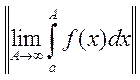 называется
несобственным интегралом
называется
несобственным интегралом ![]() на
на ![]() . 2) пусть функция
. 2) пусть функция ![]() определена
на
определена
на ![]() и интегрируема на
и интегрируема на ![]() ,
тогда предел при
,
тогда предел при ![]()
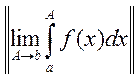 называется
несобственным интегралом
называется
несобственным интегралом ![]() на
на ![]() . 3) если предел существует и равен
конечному числу, то говорят, что несобственный интеграл сходится.
. 3) если предел существует и равен
конечному числу, то говорят, что несобственный интеграл сходится.
Критерий сходимости: пусть ![]() и
и
![]() интегрир. на
интегрир. на ![]() , и
, и ![]() ,
, ![]() . Тогда
1) если
. Тогда
1) если 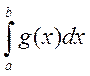 сход.
сход. 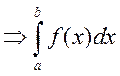 сход.
2) если
сход.
2) если 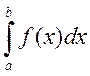 расходится
расходится 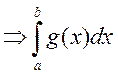 расходится.
расходится.
Доказательство: 1) ![]() пусть
пусть ![]()
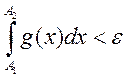 ;
; 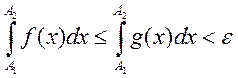 . 2)
. 2) ![]() найдутся
найдутся
![]() , такие, что
, такие, что 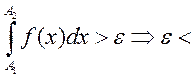
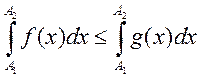 , ч.т.д. – отрицание критерия Коши =>
предела не существует.
, ч.т.д. – отрицание критерия Коши =>
предела не существует.
Определение верхней и нижней грани.
Верхние и нижние грани:
число М – верхняя граница Е, если для ![]() имеет место неравенство
имеет место неравенство ![]()
число m – нижняя граница Е, если для
![]() имеет место неравенство
имеет место неравенство ![]()
число b называется верхней гранью
множества Е, если 1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() -
верхняя граница
-
верхняя граница
число a называется нижней гранью Е,
если 1) ![]() ,
, ![]() ; 2)
; 2) ![]()
![]() -
нижняя граница.
-
нижняя граница.
Определение предела функции по Гейне и Коши, их эквивалентность.
Определение по Гейне: функция ![]() ,
имеет пределом число
,
имеет пределом число ![]() , если для любой
последовательности
, если для любой
последовательности ![]() , что
, что ![]()
Определение по Коши: функция ![]() ,
имеет предел при
,
имеет предел при ![]() , если
, если ![]() т.ч.
т.ч.
![]() ,
, ![]()
Лемма: определение предела функция ![]() по Гейне и Коши эквивалентны.
по Гейне и Коши эквивалентны.
Доказательство:
1) Пусть ![]() имеет предел
имеет предел ![]() по Коши , т.е.
по Коши , т.е. ![]() т.ч.
т.ч. ![]() . Рассмотри произвольную последовательность
. Рассмотри произвольную последовательность
![]() . Надо доказать, что
. Надо доказать, что ![]() :
: ![]() начиная
с
начиная
с ![]() все элементы
все элементы ![]() будут в
окрестности
будут в
окрестности ![]()
![]() (это из опр. по Коши)
(это из опр. по Коши) ![]() по Гейне, ч.т.д.
по Гейне, ч.т.д.
![]()
2) Пусть существует определение по Гейне, т.е. ![]()
![]() , т.е.
, т.е. ![]() имеет
имеет ![]() при
при ![]() по Гейне. Надо доказать, что
по Гейне. Надо доказать, что ![]() предположим, что это высказывание верно:
предположим, что это высказывание верно: ![]() . Возьмем
. Возьмем 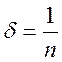 , где
, где ![]() . Т.е.
. Т.е. 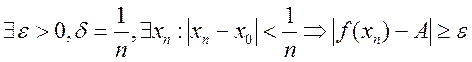 . Т.е.
мы получаем последовательность
. Т.е.
мы получаем последовательность ![]() ,
, ![]() - это противоречие опр. по Гейне, нашлась
последовательность, которая не сходится к А
- это противоречие опр. по Гейне, нашлась
последовательность, которая не сходится к А ![]() противоречие
противоречие![]() определение по Коши вытекает.
определение по Коши вытекает.
Определение производной функции: если существует
предел 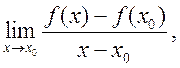 то он называется производной функции f точке x0 и обозначается
то он называется производной функции f точке x0 и обозначается ![]()
Число ![]() называется пределом
последовательности
называется пределом
последовательности ![]() , если
, если ![]() (целое
число) такое, что
(целое
число) такое, что ![]()
Принцип двойственности:
1. ![]() .
.
Доказательство: Пусть ![]()
2. ![]()
Доказательство: Пусть ![]() .
.
Свойства определённого интеграла:
1) 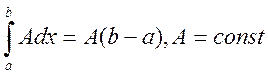
Доказательство: 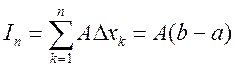
2) 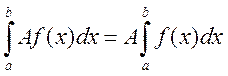
Доказательство: 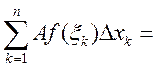
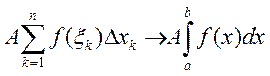
3)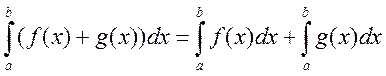
Доказательство: 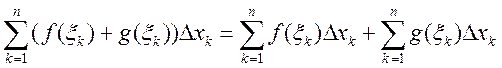
4)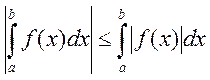
Доказательство: ![]()
5) 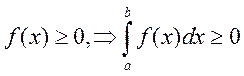
Доказательство: 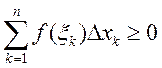
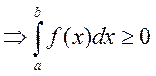
6) 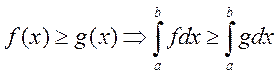
Доказательство: рассм. 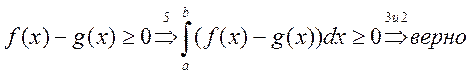
7)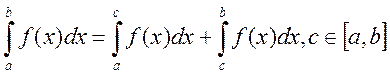
Доказательство: ![]() интегр. на
интегр. на ![]() интегр. на
интегр. на ![]() и
и ![]() . Рассм. разбиение
. Рассм. разбиение ![]() отр-ка
отр-ка
![]() , содерж. точку с .
, содерж. точку с .
Составим разность 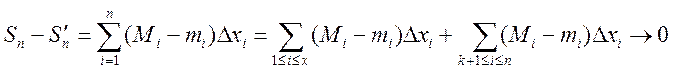 . По лемме (Дарбу)
. По лемме (Дарбу) ![]() интегр. на
интегр. на ![]() и
и ![]() . Докажем равенство:
. Докажем равенство: 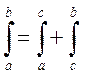 . Составим разность
. Составим разность ![]() для
раз-ий отр.
для
раз-ий отр. ![]() , включающих точку с
, включающих точку с 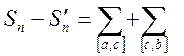
8) ![]() и непрер. на
и непрер. на ![]() и
и 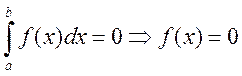
Доказательство (от противного): пусть ![]() , в кот.
, в кот. ![]() так,
что:
так,
что: 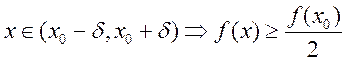 ;
; 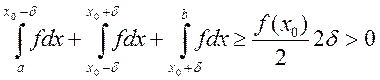
9) Теорема о среднем: ![]() -
непрерывна на
-
непрерывна на ![]()
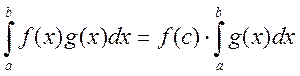 , где
, где ![]()
Доказательство: все функции интегрируемы – мы предполагаем.
Пусть М – макс. значение ![]() на
на ![]() , m – мин. значение
, m – мин. значение
![]() на
на ![]()
![]() . Интегрируем
. Интегрируем 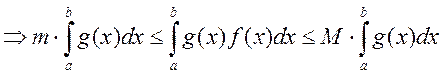 .
Пусть
.
Пусть ![]() - любая точка. Пусть
- любая точка. Пусть 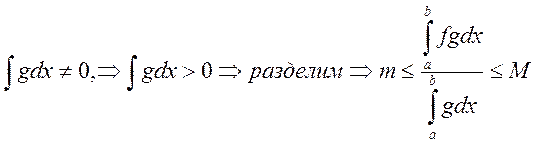 . Т.к.
. Т.к. ![]() принимает
все промежуточные значения
принимает
все промежуточные значения 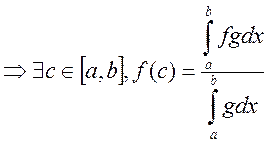
10) Неравенство Коши-Буняковского:
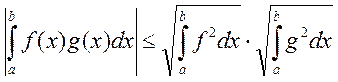
Доказательство: 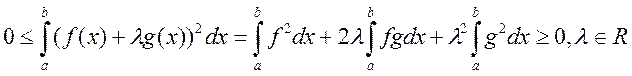 - квадратное уравнение
отн. l.
- квадратное уравнение
отн. l. 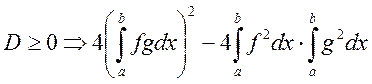
Теорема: из всякой ограниченной последовательности ![]() можно выбрать сходящуюся
подпоследовательность.
можно выбрать сходящуюся
подпоследовательность.
Доказательство: по условию имеем, что найдется
с>0 такое, что ![]() для всех n/ Разделим отрезок I0=[-c,c] пополам. Один из получившихся
отрезков содержит бесконечное число последовательности. Назовем его I1 и в качестве 1-ого члена в искомой
подпоследовательности возьмем какой-либо элемент
для всех n/ Разделим отрезок I0=[-c,c] пополам. Один из получившихся
отрезков содержит бесконечное число последовательности. Назовем его I1 и в качестве 1-ого члена в искомой
подпоследовательности возьмем какой-либо элемент ![]() , т.е.
положим
, т.е.
положим ![]() . Затем отрезок I1
снова разобьем на два и обозначим через I2
ту его половину, которая содержит бесконечно много членов последовательности
. Затем отрезок I1
снова разобьем на два и обозначим через I2
ту его половину, которая содержит бесконечно много членов последовательности ![]() . Среди них выберем такой член
. Среди них выберем такой член ![]() , номер которого n2
превосходит число n1, и положим
, номер которого n2
превосходит число n1, и положим ![]() . Повторяя описанную процедуру
применительно к отрезку I2, получим отрезок
. Повторяя описанную процедуру
применительно к отрезку I2, получим отрезок ![]() и член
и член ![]() с
условием n3>n2.
Далее таким же образом найдем
с
условием n3>n2.
Далее таким же образом найдем ![]() ,
, ![]() и т.д. В результате мы получим числовую
последовательность
и т.д. В результате мы получим числовую
последовательность ![]() и последовательность вложенных
отрезков
и последовательность вложенных
отрезков ![]() , причем
, причем ![]() при
всех
при
всех ![]() . Другими словами,
. Другими словами, ![]() будет
подпоследовательностью для
будет
подпоследовательностью для ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.