Глава 2. Предел функции
2.1. Предел функции. Основные понятия.
Пусть
функция ![]() определена в некоторой окрестности точки
определена в некоторой окрестности точки ![]() , за исключением быть может самой точки
, за исключением быть может самой точки ![]() .
.
Число A называется пределом ![]() в
точке
в
точке ![]() и пишут
и пишут 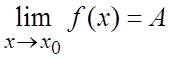 , если
для любого
, если
для любого ![]() существует
существует ![]() такое
что, для любых x таких,
что
такое
что, для любых x таких,
что ![]() выполняется
выполняется ![]() ;
;![]()
![]() .
.
Число A называется пределом ![]() при
при
![]() , если для любого
, если для любого ![]() существует
число
существует
число ![]() такое, что для любых x
таких, что
такое, что для любых x
таких, что ![]() выполняется
выполняется ![]() .
.
Теорема 1. Пусть 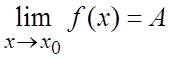 и
и 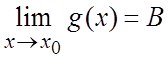 . Тогда выполняется:
. Тогда выполняется:
а) 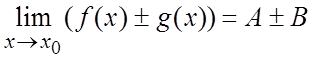 ; б)
; б)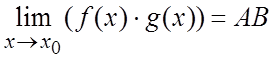 ;
;
в) 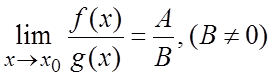 .
.
Неопределенностями
называются следующие предельные выражения: 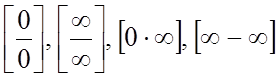 ,
, ![]() ,
, ![]() ,
, ![]() .Например, запись
.Например, запись ![]() означает,
что это есть предельное выражение для функции
означает,
что это есть предельное выражение для функции ![]() при
стремлении
при
стремлении ![]() (т.е.
(т.е. 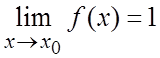 и
и 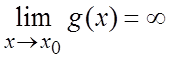 ).
).
2.2. Предел дробно-рациональной функции.
Иррациональные выражения.
При вычислении предела дробно-рациональной функции
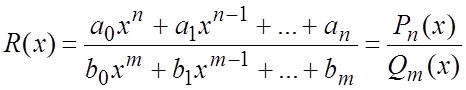 в т.
в т. ![]() применяется
метод разложения многочленов
применяется
метод разложения многочленов ![]() на множители.
на множители.
Пример. Вычислить предел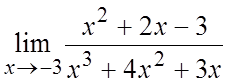 .
.
Ñ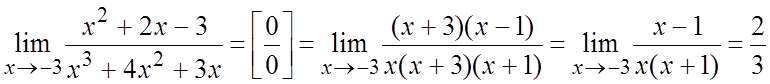 .#
.#
Вычисление
предела ![]() при
при ![]() производится
методом деления
производится
методом деления ![]() и
и ![]() на
на ![]() , где
, где ![]() .
Получаем
.
Получаем
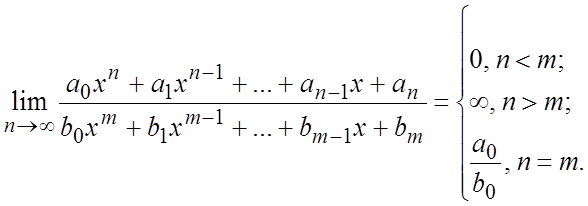
Пример. Вычислить предел 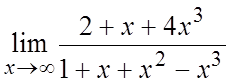 .
.
Ñ Разделим числитель и знаменатель дроби на ![]() .
.
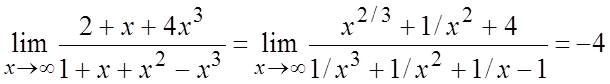 .#
.#
Метод деления на x в старшей степени применим и к пределам функций, содержащих иррациональные выражения.
Пример. Вычислить 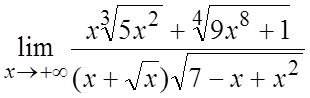 .
.
Ñ Старшая степень x
в числителе – вторая у выражения ![]() , а в знаменателе также
вторая при произведении x на
, а в знаменателе также
вторая при произведении x на ![]() . Тогда
. Тогда 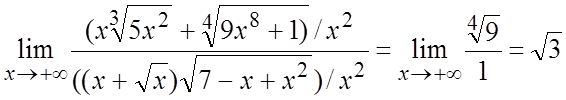 .#
.#
Часто при вычислении пределов, содержащих иррациональные выражения, применяется метод перевода иррациональности из числителя в знаменатель или наоборот.
Пример. Вычислить 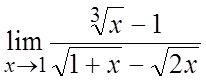 .
.
Ñ 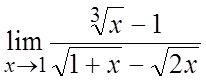 =
=![]() =
= 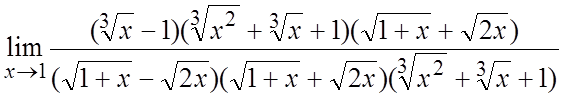 =
= 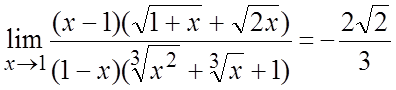 .#
.#
Пример. Вычислить 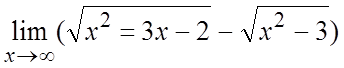 .
.
Ñ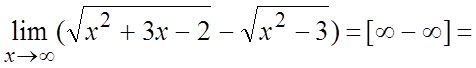 =
=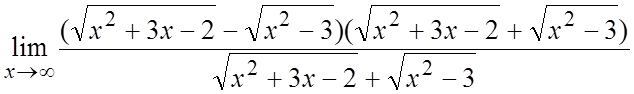 = =
= =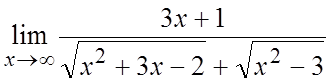 =(делим
числитель и знаменатель на x) =
=(делим
числитель и знаменатель на x) = ![]() .#
.#
Найти пределы.
1.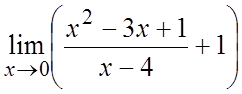 . 2.
. 2.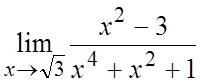 . 3.
. 3.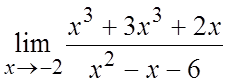 . 4.
. 4.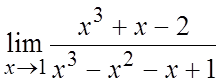 . 5.
. 5.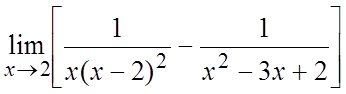 . 6.
. 6.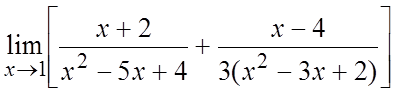 . 7.
. 7.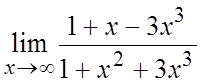 . 8.
. 8.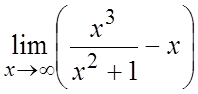 . 9.
. 9.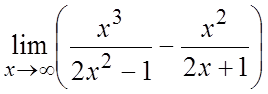 .
10.
.
10.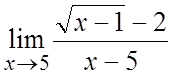 . 11.
. 11.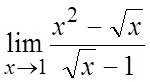 .
12.
.
12.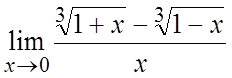 . 13.
. 13. 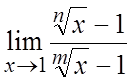 , (n и m
– целые числа). 14.
, (n и m
– целые числа). 14.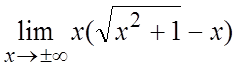 . 15.
. 15.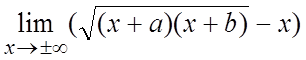 .
16.
.
16.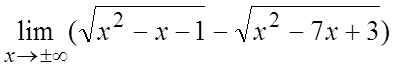 . 17.
. 17.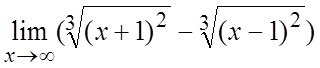 .
18.
.
18.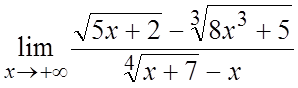 . 19.
. 19.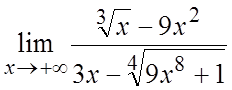 .
20.
.
20.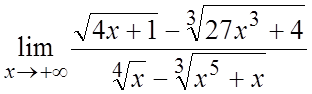 .
.
2.3. Бесконечно малые величины. Первый замечательный предел.
Функция ![]() называется бесконечно малой при
называется бесконечно малой при ![]() (б.м.), если
(б.м.), если 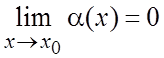 .
Пусть
.
Пусть ![]() и
и ![]() - б.м.
при
- б.м.
при ![]() . Если
. Если 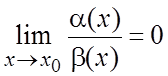 , то
, то ![]() называется бесконечно малой более
высокого порядка, чем
называется бесконечно малой более
высокого порядка, чем ![]() и пишут
и пишут ![]() ,
, ![]() . Если
. Если 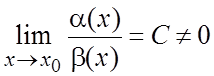
![]() , то
, то ![]() и
и ![]() называются
б.м. одного порядка малости. Если
называются
б.м. одного порядка малости. Если 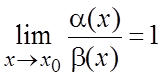 , то
, то ![]() и
и ![]() называются
эквивалентными и это обозначается
называются
эквивалентными и это обозначается ![]() при
при ![]() . Если существует число k, такое что
. Если существует число k, такое что 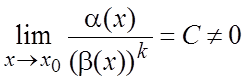 , то
, то ![]() называется б.м. порядка k относительно
называется б.м. порядка k относительно ![]() .
. ![]() называется бесконечно большой (б.б.) при
называется бесконечно большой (б.б.) при ![]() , если
, если 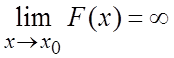 .
.
Теорема. ![]() - бесконечно малая при
- бесконечно малая при ![]()
![]()
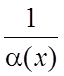 -
бесконечно большая при
-
бесконечно большая при ![]() .
.
Первый
замечательный предел – это равенство 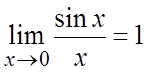 или
иначе sin x ~ x при
или
иначе sin x ~ x при ![]() .
.
Следующие б.м.
величины при ![]() - эквивалентны:
- эквивалентны:
x ~ sin x ~ tg x ~ arcsin x ~arctg x ~ (![]() )~ ln(1
+ x); 1 – cos x ~
)~ ln(1
+ x); 1 – cos x ~ ![]() ,
,
![]() ~x ln a.
~x ln a.
Если ![]() ,
, ![]() б.м.
при
б.м.
при ![]() и
и ![]() ,
, ![]() , то
, то 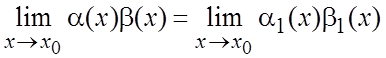 и
и 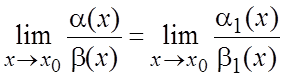 .
.
Разность б.м. величин можно заменить в пределе на разность величин им эквивалентных, только если эти величины не эквивалентны между собой.
Пример. Вычислить 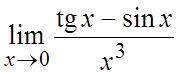 .
.
Ñ tg
x ~ sin x при ![]() ,
следовательно нельзя заменить tg x и sin x на x:
,
следовательно нельзя заменить tg x и sin x на x:
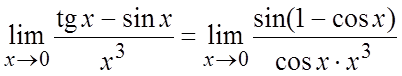 =
=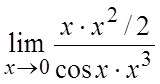 =
=![]() . #
. #
При вычислении пределов с использованием эквивалентных б.м. величин часто применяется метод замены переменной.
Пример. Вычислить 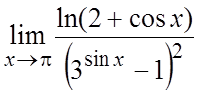 .
.
Ñ 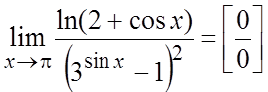 = ½замена
= ½замена ![]() ½=
½=  = =
= =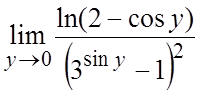 =
= 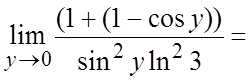
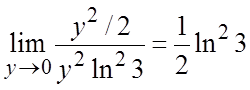 .#
.#
Найти пределы.
21.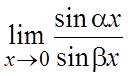 . 22.
. 22.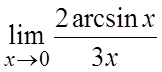 .
23.
.
23.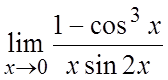 . 24.
. 24.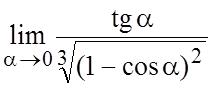 .
25.
.
25. . 26.
. 26.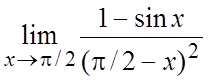 .
27.
.
27.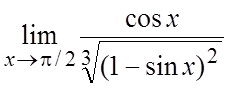 . 28.
. 28.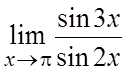 .
29.
.
29.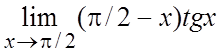 . 30.
. 30.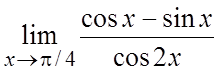 .
31.
.
31.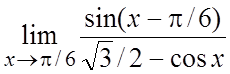 . 32.
. 32.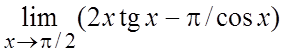 .
33.
.
33.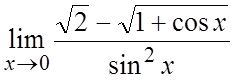 . 34.
. 34.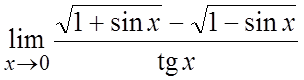 .
35.
.
35.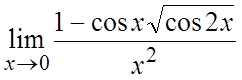 . 36.
. 36.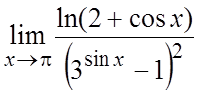 .
37.
.
37.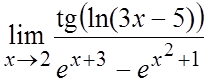 .
.
Определить
порядок относительно x функции, бесконечно малой при ![]() :
:
38.![]() . 39.
. 39.![]() . 40.
. 40.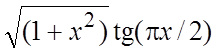 . 41.
. 41.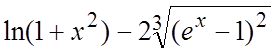 . 42.
. 42.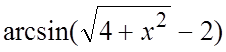 .
.
Дана функция.
Найти ей эквивалентную вида ![]() а) при
а) при ![]() ; б) при
; б) при ![]() .
.
43.![]() . 44.
. 44.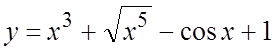 . 45.
. 45.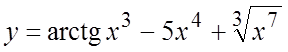 . 46.
. 46. ![]() . 47.
. 47.![]() . 48.
. 48.![]() . 49.
. 49.![]() .
.
2.4. Второй замечательный предел
Второй
замечательный предел раскрывает неопределенность ![]() :
: 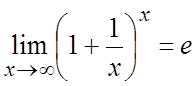 . Более обще, этот предел можно записать в
виде
. Более обще, этот предел можно записать в
виде 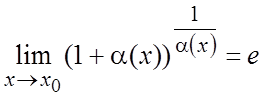 , где
, где ![]() - б.м.
при
- б.м.
при ![]() .
.
Пусть 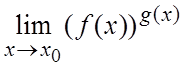 дает неопределенность вида
дает неопределенность вида ![]() . Так как
. Так как 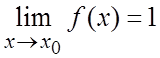 , то
, то ![]() где
где ![]() - б.м.
при
- б.м.
при ![]() . Тогда
. Тогда 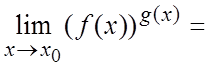 =
=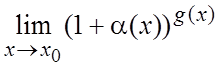 =
= 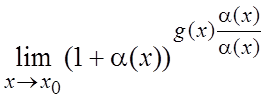 =
= 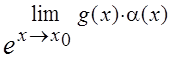 .
.
Пример. Вычислить 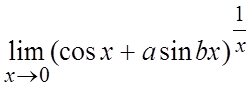 .
.
Ñ 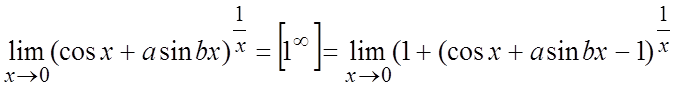 =
=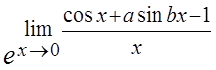 .
.
Рассмотрим 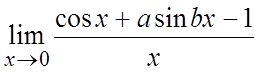 .
. ![]() при
при ![]() и
и 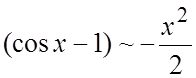 .
.
Бесконечно малые
величины ![]() и
и ![]() не
являются эквивалентными и следовательно
не
являются эквивалентными и следовательно 
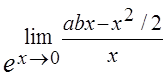 =
=![]() . #
. #
Найти пределы.
50.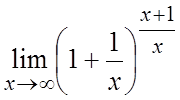 . 51.
. 51.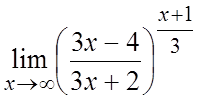 .
52.
.
52.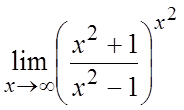 . 53.
. 53.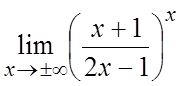 . 54.
. 54.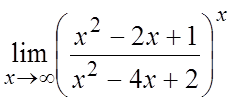 . 55.
. 55.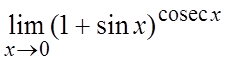 .
56.
.
56.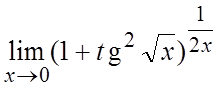 . 57.
. 57.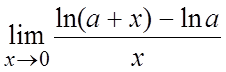 .
58.
.
58.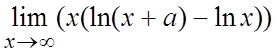 . 59.
. 59.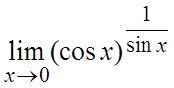 .
.
Ответы к задачам главы 2:
1. 3/4. 2.
0. 3. –2/5. 4. ![]() . 5.
. 5. ![]() . 6. 0. 7.-1. 8. 0. 9.
1/4. 10. 1/4. 11. 3. 12. 2/3. 13. m/n. 14. 1/2, если
. 6. 0. 7.-1. 8. 0. 9.
1/4. 10. 1/4. 11. 3. 12. 2/3. 13. m/n. 14. 1/2, если ![]() ; -
; -![]() , если
, если ![]() . 15.
. 15. 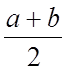 , если
, если ![]() ;
; ![]() , если
, если ![]() . 16.
. 16. ![]() . 17. 0. 18. 2. 19.
. 17. 0. 18. 2. 19. ![]() . 20. 0. 21.
. 20. 0. 21. ![]() .
22. 2/3. 23. 3/4. 24.
.
22. 2/3. 23. 3/4. 24. ![]() .
25. –1. 26. 1/2. 27.
.
25. –1. 26. 1/2. 27. ![]() .
28. –3/2. 29. 1. 30.
.
28. –3/2. 29. 1. 30. ![]() .
31. 2. 32. –2. 33.
.
31. 2. 32. –2. 33. ![]() .
34. 1. 35. 3/2. 36.
.
34. 1. 35. 3/2. 36.  .
37.
.
37. ![]() . 38. 1/2. 39. эквивалентная
б.м. 40. 1. 41. 2/3. 42. 2. 43. a)
. 38. 1/2. 39. эквивалентная
б.м. 40. 1. 41. 2/3. 42. 2. 43. a) ![]() ; ,б)
; ,б) ![]() . 44.
а)
. 44.
а) ![]() ; б)
; б) 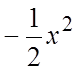 . 45.
а)
. 45.
а) ![]() б)
б) ![]() . 46. a)
. 46. a) ![]() ;
б)
;
б) ![]() . 47. а)
. 47. а) ![]() ; б)
; б) ![]() . 48. а)
. 48. а) ![]() , б)
, б) ![]() . 49. а)
. 49. а) ![]() б)
б) ![]() . 50. 1. 51.
. 50. 1. 51. ![]() .
52.
.
52. ![]() . 53. 0, если
. 53. 0, если ![]() ;
; ![]() , если
, если ![]() . 54.
. 54. ![]() . 55. a.
56. 1. 57. 1/e. 58. e.
. 55. a.
56. 1. 57. 1/e. 58. e.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.