Приближенные числа и оценка погрешностей при вычислениях

ГЛАВА 18

ПРИБЛИЖЕННЫЕ ЧИСЛА И ОЦЕНКА ПОГРЕШНОСТЕЙ ПРИ ВЫЧИСЛЕНИЯХ

18.1.   Приближенные числа. Классификация погрешностей

 Пусть А — точное ( вообще говоря, неизвестное ) значение некоторой величины, а- известное приближенное значение этой же величины . Погрешностью (ошибкой) приближенного числа а называется разность  между точным и приближенным значениями.

Простейшей количественной мерой ошибки является абсолютная погрешность  приближенного числа а:

                                                                                                                    (1.1)

Поскольку точное число А, как правило, неизвестно, то непосредственное вычисление  невозможно и пользуются верхними границами для .

Предельной абсолютной погрешностью  приближенного числа а называется число, не меньшее абсолютной погрешности этого числа, т. е. . Следовательно,

                                                     ,                                            (1.2)

т.е.  является приближением числа А по недостатку, а - приближением числа А по избытку. Формулу (1.2) кратко записывают в виде .

Пример 1. Определить предельную абсолютную погрешность числа а=3,14, взятого в качестве приближенного значения числа .

Известно, что . От сюда следует, что  За предельную абсолютную погрешность можно принять число . Если же учесть, что 3,14<<3.142, то получим лучшую оценку ; . #

Знания только абсолютной погрешности для характеристики качества измерения. Пусть, например, при взвешивании двух тел получили следующие результаты: ; . Хотя абсолютные погрешности обоих результатов одинаковы, качество измерения в первом случае лучше чем во втором.

Относительной погрешностью приближенного числа а называется отношение абсолютной погрешности  этого числа к модулю соответствующего точного числа А (), т.е.                     

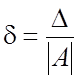                                                                                                                          (1.3)

Предельной относительной погрешностью приближенного числа а называется число , не меньшее относительной погрешности этого числа, т. е. .Следовательно, можно считать

                                                             ,                                                    (1.4)

Если принять , то формула (1.4) примет вид

                                                            ,                                                      (1.5)

а точное число А лежит в границах

                                                     ,                                      (1.6)

Предельную относительную погрешность принято выражать в процентах .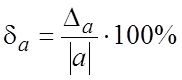

 18.2.   ЗНАЧАЩАЯ ЦИФРА.  ЧИСЛО ВЕРНЫХ ЗНАКОВ

Всякое число а может быть представлено в виде конечной или бесконечной суммы слагаемых

                     ,                     (2.1)

где - цифры числа а ( = 0, 1, 2, ..., 9), т - некоторое целое число, называемое старшим десятичным разрядом числа а. Например, число 396,47 может быть представлено в виде

                               .

При проведении реальных вычислений всякое число, имеющее вид бесконечной суммы слагаемых, заменяется на сумму конечного числа слагаемых, т. е. вместо суммы (2.1) записывают сумму  ()

                                .                 (2.2)

Значащими цифрами приближенного числа b называются все сохраняемые десятичные знаки  (причем ), а все остальные знаки могут принимать и нулевые значения. Например,

                               

                              

имеют соответственно 4 и 6 значащих цифр. Если в данном числе 0,073040 последняя цифра не является значащей, то число должно быть записано в виде 0,07304.

По виду чисел при обычной их записи трудно судить о точном количестве

значащих цифр этих чисел, однако этой неопределенности можно избежать следующим образом. Например, если число 827000 имеет три значащие цифры, то его следует записать в виде , если же оно имеет четыре значащие цифры, то в виде .

Первые п значащих цифр приближенного числа называются верными, если абсолютная погрешность этого числа не больше половины единицы разряда, выражаемого - й значащей цифрой. Например, для точного числа  А = 14,298 число а = 14,300 является приближенным числом с четырьмя верными знаками, так как

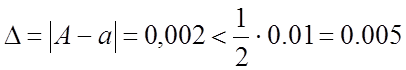
Число верных знаков приближенного числа связано с относительной погрешностью этого числа соотношением.

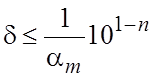                                                             ,                                                (2.3)

где - относительная погрешность приближенного числа а, n- число верных знаков числа; - первая значащая цифра числа а.

Из формулы (2.3) следует, что в качестве предельной относительной погрешности числа а можно взять величину

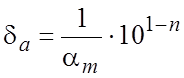                                                            .                                             (2.4)

Если число верных знаков , то справедлива формула

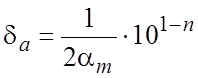                                                         .                                            (2.5)

Пример 2. Найдем предельную относительную погрешность, если точное число 14,298 заменяется приближенным 14,300. В данном случае , п = 4. По формуле (2.5) имеем

.

Пример 3. Определим число десятичных знаков  при относительной погрешности . Очевидно, что . Тогда, согласно формуле (2.5) 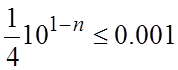, т.е. .

 18.3.   ПРАВИЛА ОКРУГЛЕНИЯ

Округлением данного числа а (точного или приближенного) называется замена его числом b с меньшим количеством значащих цифр. Эта замена производится таким образом, чтобы погреш­ность округления а-b  была минимальной.