

















1 и 2 теоремы Вейерштрасса
Первая теорема Вейерштрасса : Всякая непрерывная
функция ![]() , заданная на отрезке
, заданная на отрезке ![]() , ограничена, т.е.
, ограничена, т.е. ![]() числа
m и M такие, что
числа
m и M такие, что ![]() .
.
Доказательства: Докажем ограниченность сверху, т.к. снизу аналогично!!!
1) ![]() -ограничена сверху,
-ограничена сверху, ![]() - это надо доказать. Предположим, что это
неверно.
- это надо доказать. Предположим, что это
неверно.
2) т.е. ![]() , такое что
, такое что ![]()
3) Возьмем ![]() , что
, что ![]()
4) Меняем ![]() получаем
последовательность
получаем
последовательность ![]() . Выделяем сходящуюся
подпоследовательность:
. Выделяем сходящуюся
подпоследовательность: ![]()
![]()
5) т.к. ![]() - непрерывная
- непрерывная![]()
6) Если в 3) взять n=1 , ![]() но
но ![]() ,
противоречие => 2) – не верно т.к. верно1) => теорема доказана для M, а для m – аналогично
,
противоречие => 2) – не верно т.к. верно1) => теорема доказана для M, а для m – аналогично
Вторая теорема Вейерштрасса: Всякая непрерывная
функция![]() , достигает своих наибольшего и наименьшего
значений, т.е. если
, достигает своих наибольшего и наименьшего
значений, т.е. если 
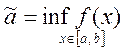 , то
, то ![]()
![]() и
и ![]()
![]() , что
, что ![]() а
а ![]()
Доказательство: Только для sup,
т.к. inf аналогично. Надо доказать, что![]()
![]() , такие что
, такие что ![]() где
где ![]() .
Допустим, такой точки нет, т.е.
.
Допустим, такой точки нет, т.е. ![]() . Рассмотрим
. Рассмотрим 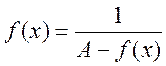 ,
, ![]() для
для ![]() по построению и
по построению и ![]() -
непрерывна, т.к. 1-непрерывна и разность тоже =>
-
непрерывна, т.к. 1-непрерывна и разность тоже => ![]() -непрерывна
=> по 1-ой теореме Вейерштрасса она ограничена сверху, т.е.
-непрерывна
=> по 1-ой теореме Вейерштрасса она ограничена сверху, т.е. ![]() А1>0, что
А1>0, что ![]()
![]() , подставим вместо
, подставим вместо ![]()
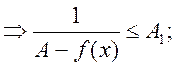
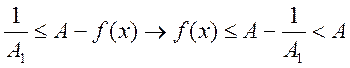
Аксиомы вещественных чисел:
Аксиомы ![]() чисел. R – это произвольное множество, в котором определены
операции,
чисел. R – это произвольное множество, в котором определены
операции, ![]() операции сравнения
операции сравнения ![]()
Аксиомы поля:
1. ![]()
2. ![]()
3. ![]() что
что
![]()
4. ![]() ,
что
,
что ![]()
5. ![]()
6. ![]()
7. ![]() что
что
![]()
8. ![]() что
что ![]()
9. ![]()
Упорядоченное поле:
1. Из ![]()
2. Если ![]()
3. ![]() либо
либо ![]() , либо
, либо ![]()
4. если ![]()
5. ![]()
Архимедово поле
![]() целое
целое ![]()
Аксиома непрерывности: ![]() -
вложенные отрезки,
-
вложенные отрезки, ![]() и
и ![]() .
.  Æ -
это значит, что на прямой нет дырок
Æ -
это значит, что на прямой нет дырок
Выпуклые функции: веществ. функция ![]() , B – выпуклое
множество, называется выпуклой, если выполняется неравенство:
, B – выпуклое
множество, называется выпуклой, если выполняется неравенство: ![]() для
для ![]() где
где 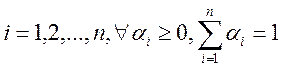 . Если n=2 , то
будем рассм. формулу Иенсена.
. Если n=2 , то
будем рассм. формулу Иенсена.
Теорема: пусть функции ![]() и
и ![]() - непрер. диф-мые на
- непрер. диф-мые на ![]() выполняется
выполняется ![]()
Доказательство: 1) ![]() - по
определению,
- по
определению, ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]()
γ- и β-функции.
Определение: Эйлеров интеграл первого рода. Так называется ( по предложению Лежандра) интеграл вида:
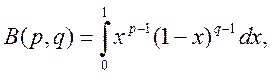 где p, q>0.
где p, q>0.
Он представляет функцию от двух переменных параметров p и q: функцию B(«Бета»).
Определение: Эйлеров интеграл второго рода. Это название было присвоено Лежандром замечательному интегралу:
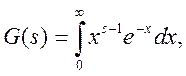
Который сходится при любом s>0 и определяет функцию G («Гамма»).
Докажем, что: 1. G(s+1)=s*G(s);
2. 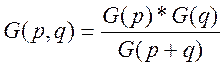
G(1)=1; G(2)=G(1)=1; G(3)=2*G(1)=2!;…;
G(n+1)=n!,
n![]() N, то есть G-это аналог факториала, а B- аналог
биномиального коэффициента.
N, то есть G-это аналог факториала, а B- аналог
биномиального коэффициента.
Доказательство:
1.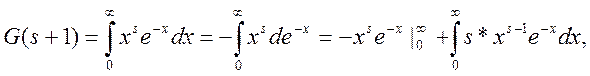 где
где ![]() в
пределе
в
пределе ![]()
2. Рассмотрим
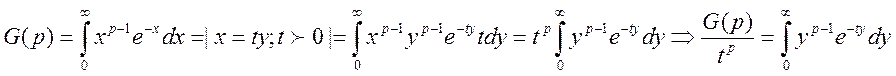
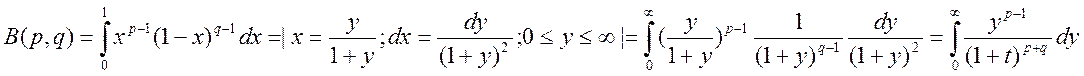
Составим 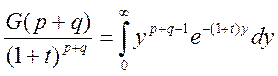 и
проинтегрируем по t
и
проинтегрируем по t![]()
Левую: 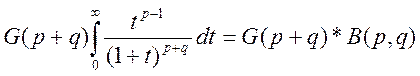
Правую: 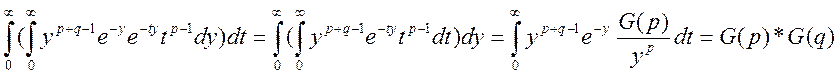 ,
все доказано, так как G(p+q)*B(p,q)=G(p)*G(q)
,
все доказано, так как G(p+q)*B(p,q)=G(p)*G(q)
Классы интегрируемых функций.
Теорема 1:.Если функция f(x) – непрерывна на отрезке [a,b], то она интегрируема на [a,b].
Доказательство:Составим
разность: Sn-Sǹ
= ![]() (Mk - mk )∆xk =
(Mk - mk )∆xk = ![]() (f(ξk) - f(ξ
̀k)) ∆xk
(f(ξk) - f(ξ
̀k)) ∆xk
Т.к. функция f(x) – непрерывна на [a,b] => f(x)
– непрерывна на [xk-1,xk] => $ ξ̀k и ξ ̀k Î [xk-1,xk], что Mk = f(ξk),
mk = f(ξ ̀k) Т.к. f(x) непрерывна на [a,b] => равномерно непрерывна на [a,b] => для ![]() e >0 $ d, что ½x - x'½< d => ½
f(x) - f(x')½< e Возьмём разбиение мелкости ln< d => ½
e >0 $ d, что ½x - x'½< d => ½
f(x) - f(x')½< e Возьмём разбиение мелкости ln< d => ½![]() (f(ξk) - f(ξ
̀k)) ∆xk ½£ e×
(f(ξk) - f(ξ
̀k)) ∆xk ½£ e×![]() ∆xk
= e×(b-a)®0 теорема доказана!!!
∆xk
= e×(b-a)®0 теорема доказана!!!
Теорема 2: Монотонная, ограниченная функция f(x) на отрезке [a,b], интегрируема.
Доказательство: Монотонная =>
x £ x' => f(x) £ или ³ f(x')
Пусть f(x) – монотонно
неубывающая функция => êSn- Sn ̀ê=![]() (Mk - mk )∆xk , Mk = f(xk),
mk = f(xk-1) =>
(Mk - mk )∆xk , Mk = f(xk),
mk = f(xk-1) =>
êSn- Sn ̀ê=![]() ( f(xk) - f(xk-1))∆xk£ êêпусть мелкость разбиения ln< e => ∆xk £ ln £ e êê£ e×
( f(xk) - f(xk-1))∆xk£ êêпусть мелкость разбиения ln< e => ∆xk £ ln £ e êê£ e×![]() ( f(xk) - f(xk-1))∆xk = e×(f(b)-f(a)), а т.к. e -
произвольное => êSn- Sn ̀ê
( f(xk) - f(xk-1))∆xk = e×(f(b)-f(a)), а т.к. e -
произвольное => êSn- Sn ̀ê![]() 0, при ln ® 0, Ч.Т.Д.
0, при ln ® 0, Ч.Т.Д.
Критерий Коши – существование предела: для того чтобы
![]() имела конечный предел при
имела конечный предел при ![]() , необходимо и достаточно, чтобы для
, необходимо и достаточно, чтобы для ![]() , что для всех
, что для всех ![]() и
и ![]() и таких, что
и таких, что ![]() .
Доказывается сведением к последовательности.
.
Доказывается сведением к последовательности.
Критерий Коши:для того чтобы
последовательность ![]() сходилась, необходимо и
достаточно, чтобы она была фундаментальной.
сходилась, необходимо и
достаточно, чтобы она была фундаментальной.
Доказательство: Необходимость. если  , то для любого
, то для любого ![]() существует
существует
![]() , такое, что для всякого
, такое, что для всякого ![]() имеем
имеем ![]() .
.
Следовательно, для любых ![]()
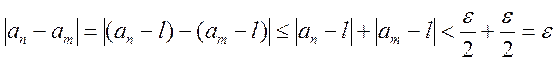 .
.
Поэтому ![]() - фундаментальная
последовательность.
- фундаментальная
последовательность.
Достаточность. По условию последовательность ![]() является фундаментальной.
является фундаментальной.
1. Докажем, что ![]() ограничена. В самом
деле, возьмем
ограничена. В самом
деле, возьмем ![]() =1. Тогда найдется n0=n0(1) такое,
что для всех
=1. Тогда найдется n0=n0(1) такое,
что для всех ![]() имеем
имеем ![]() . Но
тогда
. Но
тогда ![]() . Отсюда
. Отсюда ![]() .
.
2. В силу теоремы Больцано-Вейерштрасса существует
сходящаяся подпоследовательность ![]() при
при ![]() . Условие её сходимости можно записать так:
. Условие её сходимости можно записать так:
![]()
![]()
![]() такое
что
такое
что ![]() имеем
имеем ![]() . Пусть
. Пусть
![]() и
и ![]() .
Тогда для всех n>N и nk>N имеем
.
Тогда для всех n>N и nk>N имеем 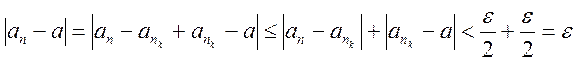 , т.е. последовательность
, т.е. последовательность ![]() сходится.
сходится.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.