Основы химической кинетики. Формальная кинетика простых и сложных реакций. Реакции в открытых системах. Механизм элементарного химического превращения, страница 9

7.  Ядерная статсумма:

так как активированный комплекс содержит те же ядра, что и исходные вещества, то ядерная статсумма сокращается, учитывать ее нет необходимости.

Величина , фигурирующая в формуле метода переходного состояния, называется частотным фактором.

5.7. Мономолекулярные реакции

Рассмотрим мономолекулярную реакцию в пределе высоких давлений.

Константа скорости такой реакции

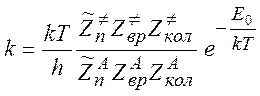
В пределе низких температур колебательные статсуммы заморожены: , и

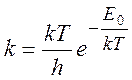
В пределе высоких температур колебательные статсуммы сильно разморожены: , и

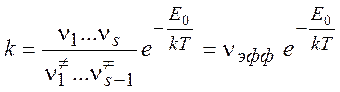
Если активированный комплекс более  “рыхлый”, чем исходная молекула, - аномально высокий предэкспонент. Если активированный комплекс более  “жесткий”, чем исходная молекула, - аномально низкий предэкспонент.

5.8. Бимолекулярные реакции

В случае “рыхлого” активированного комплекса выражение для константы скорости совпадает с предсказанием по теории столкновений (модель линии центров). В случае “жесткого” активированного комплекса появляется стерический множитель (порядка 10^-2).

Глава 6. Типы элементарных реакций

6.1. Основные понятия

1.  Реакции, протекающие с разрывом или (и) образованием одной связи.

2.  Реакции, протекающие с разрывом или (и) образованием нескольких связей.

Гомолитические реакции – если разрываются или (и) образуются электронные пары (радикалы). Гетеролитические реакции – если электронные пары не разрываются или (и) не образуются (ионы).

6.2. Радикальные реакции

1)  Распад молекулы на свободные радикалы, рекомбинация радикалов.

2)  Образование радикалов при реакциях насыщенных молекул.

3)  Радикальные реакции замещения.

4)  Реакции присоединения радикалов.

Глава 7. Реакции в жидкости

7.1.  Основные понятия

Нормальные жидкости – макроскопически однородны и изотропны. Основные отличия от газа:

1)  сильное межмолекулярное взаимодействие;

2)  жидкость занимает собственный объем;

3)  эффект “клетки”

7.2.  Химическая реакция и диффузия

Рассмотрим бимолекулярную реакцию в жидкости:

Пусть  и  - радиусы молекул A и B;   и  - коэффициенты диффузии этих молекул. Выберем начало координат в центре молекулы A и примем ее радиус равным . Тогда  молекулы B можно рассматривать как точечные, имеющие коэффициент диффузии. В установившемся стационарном режиме, скорость химической реакции равна диффузионному потоку  точечных молекул B на сферическую молекулу A на расстоянии  R  от ее центра. При этом концентрация молекул B на расстоянии R равна

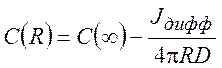                                                                                                     (7.1)

Для диффузионного потока имеем

                                                                                                               (7.2)

Отсюда следует, что

                                                                                                        (7.3)

где

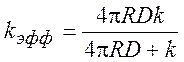                                                                                                           (7.4)

Из этой формулы видно, что существует два крайних случая – диффузионый предел и кинетический предел для реакции.

Более детальное рассмотрение процесса диффузии при наличии реакции позволяет определить характерное время установления стационарного режима, когда начинает работать формула (7.4):

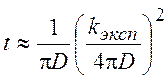                                                                                                             (7.5)

7.3.  Эффект “клетки”

Эффект “ клетки” описывается обычно посредством следующей кинетической схемы:

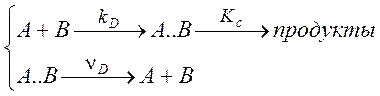                                                                          (7.6)

Для получаем:

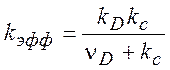                                                                                                                                                                        (7.7)