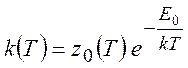Основы химической кинетики. Формальная кинетика простых и сложных реакций. Реакции в открытых системах. Механизм элементарного химического превращения, страница 7

                                                                                                          (5.5)

Для типичных величин (см²,  ,  см/с) - см³/с.

С геометрической точки зрения не каждое столкновение благоприятно для протекания реакции. В простейшей теории столкновений это учитывается введением стерического множителя, который в рамках этой теории не рассчитывается.Значение стерического множителя может быть в пределах 1 > p >10^-5,

5.4. Мономолекулярные реакции. Схема Линдемана

Процесс распада (диссоциации) молекулы можно разбить на две стадии – процессы активации и дезактивации молекулы при столкновениях и процесс распада активных молекул:

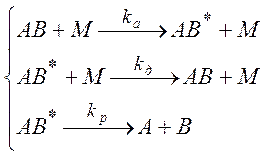                                                                                             (5.6)

В рамках приближения Линдемана считается, что скорость распада активных молекул не зависит от внутренней энергии активной молекулы. Применяя условие квазистационарности концентраций активных молекул, для скорости процесса получим

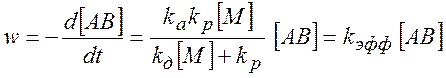                                                               (5.7)

Из этого следует, что эффективная константа скорости зависит от давления.

5.5. Метод переходного состояния

Метод переходного состояния (активированного комплекса) был сформулирован в 1935 г. (Эйринг, Эванс и Поляни, Пельцер и Вигнер). Этот метод базируется на следующих предположениях:

1)  существует адиабатическая поверхность ППЭ, которая определяет динамику движения ядер в ходе реакции;

2)  фазовое пространство реагирующей системы делится критической поверхностью  на области, отвечающие исходным веществам и продуктам реакции, при этом считается, что реакция произошла, если изображающая точка пересекает эту поверхность, скорость реакции отождествляется с потоком изображающих точек через критическую поверхность;

3)  функция распределения по координатам и импульсам для изображающих точек, пересекающих критическую поверхность в направлении реакции, считается равновесной.

По определению, переходным состоянием (активированным комплексом) называется состояние системы. Когда изображающая точка находится на критической поверхности.

Рассмотрим, например, бимолекулярную реакцию, хотя приведенный ниже вывод и его результат справедлив для любой реакции. Критическая поверхность проходит через вершину активационного барьера и перпендикулярно координате реакции. Выделим вблизи критической поверхности слой толщиной . Будем считать величину  малой: . Пусть в сосуде объема V  имеется N_A молекул A и N_B молекул B. Обозначим через  полное число пар реагирующих молекул A и B , состояние которых попадает в слой . Нас интересует, какое количество изображающих точек пересекает критическую поверхность за единицу времени – это и будет число актов реакции, происходящих в сосуде в единицу времени. Изображающие точки движутся в различных направлениях с разными скоростями в соответствии с максвелловским распределением. Интерес представляет их движение вдоль координаты реакции. Доля таких точек, двигающихся со скоростью , равна

                                                                                                   (5.8)

где  - распределение Максвелла

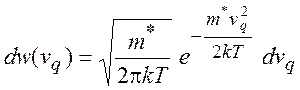                                                                                        (5.9)

здесь  - эффективная масса для движения вдоль координаты реакции. Изображающие точки, двигающиеся со скоростью , проходят длину  и пересекают критическую поверхность за время 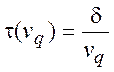. Следовательно, их поток через эту поверхность равен

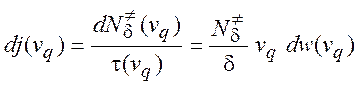                                                                           (5.10)

Полный поток:

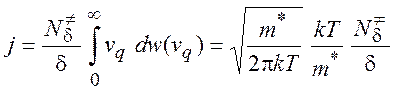                                                                      (5.11)