Решение этого уравнения при начальном условии ![]() :
:
![]() (2.3)
(2.3)
Кинетику первого порядка можно наблюдать также в случае, когда реакция имеет первый порядок по некоторому реагенту, а остальные реагенты берутся в большом избытке и изменением их концентраций по ходу процесса можно пренебречь (условия псевдопервого порядка). В каталитических реакциях также может наблюдаться кинетика первого порядка, так как катализатор не расходуется.
2.2. Необратимая реакция второго порядка
![]() (2.4)
(2.4)
Скорость реакции второго порядка
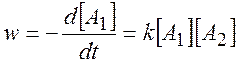 (2.5)
(2.5)
Начальные условия ![]() ,
, ![]() .
.
Введем понятие глубины превращения x:
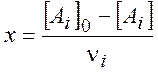 (
(![]() - стехиометрический коэффициент)
(2.6)
- стехиометрический коэффициент)
(2.6)
Для реакции (2.4) имеем
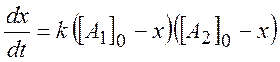 (2.7)
(2.7)
Решение этого уравнения
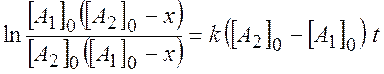 (2.8)
(2.8)
При равных начальных концентрациях реагентов решение выглядит так:
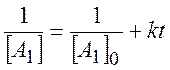 (2.9)
(2.9)
Если протекает реакция типа
![]() (2.10)
(2.10)
то решение имеет вид
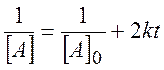 (2.11)
(2.11)
2.3. Необратимая реакция третьего порядка
![]() (2.12)
(2.12)
Скорость реакции
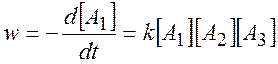 (2.13)
(2.13)
Для степени превращения x получаем дифференциальное уравнение
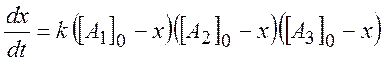 (2.14)
(2.14)
Решение этого уравнения в случае равных начальных концентраций:
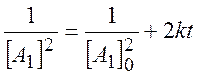 (2.15)
(2.15)
Для реакции
![]() (2.16)
(2.16)
получаем
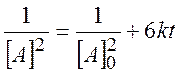 (2.17)
(2.17)
2.4. Обратимые реакции
Рассмотрим простой случай
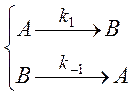 (2.18)
(2.18)
Этой кинетической схеме соответствует следующая система дифференциальных уравнений:
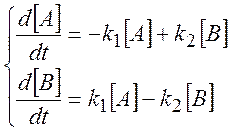 (2.19)
(2.19)
Решение этой системы:
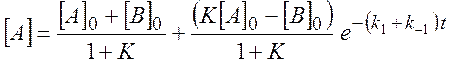 (2.20)
(2.20)
где
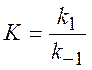 (константа
равновесия)
(2.21)
(константа
равновесия)
(2.21)
2.5. Принцип детального равновесия
Уравнения движения, описывающие процесс столкновения молекул, обратимы во времени. Это приводит к важному следствию: вероятность перехода из некоторого начального состояния в некоторое конечное состояние равна вероятности обратного перехода (принцип детального равновесия).
С учетом плотности начальных и конечных состояний принцип детального равновесия приводит к следующему выражению для связи сечений прямой и обратной бимолекулярной реакции
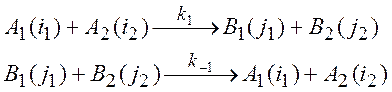 (2.22)
(2.22)
![]() (2.23)
(2.23)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - относительные импульсы и скорости
молекул до и после столкновения (
- относительные импульсы и скорости
молекул до и после столкновения (![]() ,
,![]() ).
При этом импульсы т скорости связаны законом сохранения энергии
).
При этом импульсы т скорости связаны законом сохранения энергии
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.