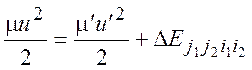Основы химической кинетики. Формальная кинетика простых и сложных реакций. Реакции в открытых системах. Механизм элементарного химического превращения, страница 4

                                                                                             (2.24)

        (изменение внутренней энергии сталкивающихся молекул)

Выражение (2.23) справедливо, если внутренние состояния молекул невырожденные. В случае вырожденных состояний справедлива формула

                                                    (2.25)

где , , ,  - степени вырождения состояний реагентов и продуктов.

В случае максвелловского распределения по скоростям:

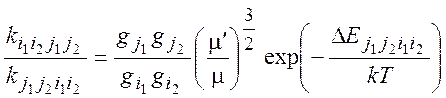                                                             (2.26)

Аналогичным образом могут быть получены соотношения между константами скорости прямого и обратного процессов при любой степени их детализации (при условии равновесного распределения по всем остальным степеням свободы).

Глава 3. Формальная кинетика сложных реакций

3.1. Последовательные и параллельные реакции

Две реакции называются последовательными, если продукт первой реакции является исходным веществом для второй. Например,

Реакции называются параллельными, если в каждой из них принимает участие хотя бы одно общее исходное вещество. Например,

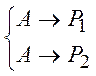
Параллельно-последовательными называются реакции, параллельные по одному веществу и последовательные по другому:

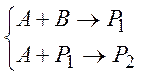
Для описания кинетики сложных реакций используется закон действующих масс для каждой элементарной стадии и принцип независимости элементарных стадий.

Принцип независимости элементарных стадий состоит в том, что скорость образования или расходования какого-либо вещества может быть представлена в виде суммы вкладов от различных элементарных реакций, т.е. протекание одной элементарной реакции не влияет на протекание другой.

Рассмотрим пример – цепь необратимых последовательных реакций первого порядка

                                                                                 (3.1)

Закон действующих масс и принцип независимости элементарных стадий приводит к системе дифференциальных уравнений первого порядка:

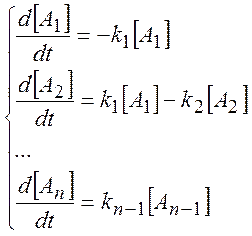                                                                                               (3.2)

или в матричном виде

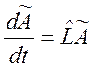                                                                                                                          (3.3)

Эта система линейных дифференциальных уравнений интегрируется стандартным методом. Из характеристического уравнения

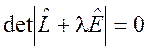                                                                                                                 (3.4)

находятся собственные значения  , , … ,  , и решение может быть представлено (для простоты собственные значения  считаются различными) в виде

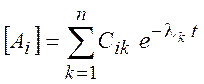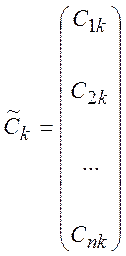 ,                                                                                (3.4)

где   - собственные векторы – решения уравнения

                                                                                                             (3.5)

3.2. Метод квазистационарных концентраций

Схема применения метода квазистационарных концентраций:

1)  выделяем короткоживущие промежуточные вещества B_i ;

2)  полагаем концентрации этих веществ стационарными: ;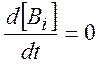

3)  из полученных алгебраических уравнений выражаем концентрации веществ B_i  через концентрации остальных веществ;

4)  решаем упрощенную систему дифференциальных уравнений (с меньшим числом переменных);

5)  оцениваем время установления квазистационарных концентраций и проверяем, выполняется ли условие, что время жизни  B_i  много меньше времени протекания реакции.

3.3. Лимитирующая стадия сложного процесса

Рассмотрим реакцию

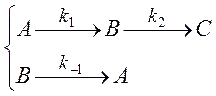                                                                                                     (3.6)

Записываем систему дифференциальных уравнений:

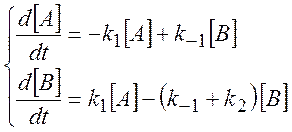                                                                                         (3.7)