Например, эндоэргическая
реакция колебательно возбужденной молекулы HCl (v) с атомом Br является эндотермической при уровне колебательного
возбуждения v<2, и экзотермической при ![]() (v –
колебательное квантовое число).
(v –
колебательное квантовое число).
1.12. Дифференциальное сечение реакции
Наиболее детальной характеристикой бимолекулярной химической реакции является дифференциальное сечение реакции, определяемое следующим образом.Рассмотрим бимолекулярную реакцию
![]() (1.9)
(1.9)
Рассмотрим следующий эксперимент – пучок частиц ![]() сталкивается с пучком частиц
сталкивается с пучком частиц ![]() с относительной скоростью u в системе центра масс
с относительной скоростью u в системе центра масс
![]() ,
, ![]()
Какое число элементарных реакций в единицу времени
протекает в единице объема, приводящих к разлету реагентов в элемент телесного
угла ![]() вблизи
вблизи ![]() ? Это
число равно
? Это
число равно
![]() (1.10)
(1.10)
Коэффициент пропорциональности ![]() называется
дифференциальным сечением реакции. Зная дифференциальное сечение
реакции, можно получить остальные (менее детальные) характеристики. Для этого
нужно усреднять по начальным состояниям и суммировать по конечным состояниям.
называется
дифференциальным сечением реакции. Зная дифференциальное сечение
реакции, можно получить остальные (менее детальные) характеристики. Для этого
нужно усреднять по начальным состояниям и суммировать по конечным состояниям.
Например, найдем сечение реакции
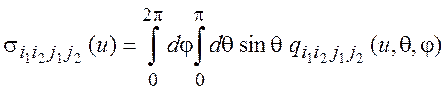 (1.11)
(1.11)
Рассмотрим теперь случай, когда есть распределение
реагирующих молекул по скоростям. Выделим подансамбль молекул ![]() , движущихся со скоростями вблизи
, движущихся со скоростями вблизи ![]() в интервале
в интервале ![]() , и
молекул
, и
молекул ![]() , движущихся со скоростями вблизи
, движущихся со скоростями вблизи ![]() в интервале
в интервале ![]() . Пусть
. Пусть ![]() и
и ![]() -
функции распределения молекул
-
функции распределения молекул ![]() и
и ![]() по скоростям. Тогда плотность подансамблей
будет
по скоростям. Тогда плотность подансамблей
будет
![]() ,
, ![]() (1.12)
(1.12)
За счет этих выделенных молекул в единице объема в единицу времени происходит следующее число актов реакции:
![]() (1.13)
(1.13)
Интегрируя по скоростям, получим константу скорости детального процесса
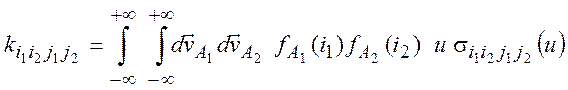 (1.14)
(1.14)
Если мы желаем получить константу скорости процесса
![]() (1.15)
(1.15)
то необходимо усреднить по функциям распределения реагентов по внутренним степеням свободы:
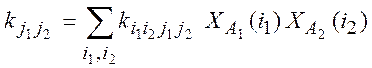 (1.16)
(1.16)
Для получения полной константы скорости процесса
![]() (1.17)
(1.17)
необходимо просуммировать по всем конечным состояниям:
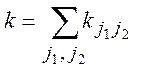 (1.18)
(1.18)
Если распределение по скоростям максвелловское, то
![]() (1.19)
(1.19)
где
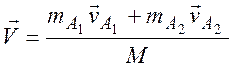
![]()
![]()
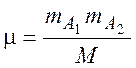
Используя явный вид распределения Максвелла
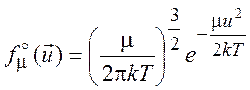 ,
, ![]() (1.20)
(1.20)
и переходя к относительной поступательной энергии реагентов
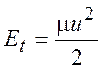 (1.21)
(1.21)
получим
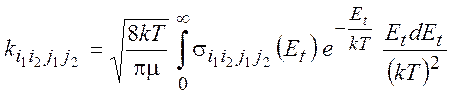 (1.22)
(1.22)
Заметим, что 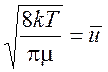 - средняя
относительная скорость реагентов. Таким образом, выражение (1.22) можно
записать иначе (опуская индексы):
- средняя
относительная скорость реагентов. Таким образом, выражение (1.22) можно
записать иначе (опуская индексы):
![]() (1.23)
(1.23)
где ![]() - сечение реакции.
- сечение реакции.
Глава 2. Формальная кинетика простых реакций
2.1. Необратимая реакция первого порядка
![]() (2.1)
(2.1)
Например, реакция изомеризации
![]()
или мономолекулярный распад
![]()
Скорость мономолекулярной реакции:
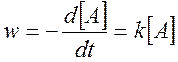 (2.2)
(2.2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.