Основы химической кинетики. Формальная кинетика простых и сложных реакций. Реакции в открытых системах. Механизм элементарного химического превращения, страница 6

Простейший реактор идеального вытеснения – трубка постоянного сечения. При этом предполагается, что все переменные – концентрации веществ и скорость потока – постоянны в каждом фиксированном сечении трубы и зависят только от одной координаты x. Уравнение (4.10) в этом случае имеет следующий вид:

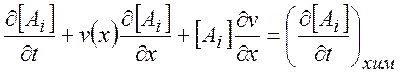                                                                     (4.11)

Мы будем рассматривать только стационарный режим реактора:

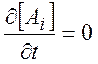                                                                                                                       (4.12)

 Рассмотрим реакцию изомеризации

Учитывая (4.12), уравнение (4.10) дает:

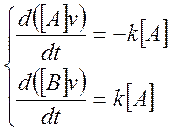                                                                                                           (4.13)

Решение имеет вид:

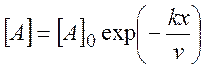                                                                                                     (4.14)

Глава 5. Механизм элементарного химического превращения

5.1. Приближение Борна-Оппенгеймера

Рассмотрим бимолекулярную реакцию

Для нахождения константы скорости этой реакции необходимо решить полную квантово-механическую задачу о движении всех ядер и электронов, содержащихся в этих молекулах. Данная задача является очень сложной даже для простейших систем. Однако, из-за большого различия в массах ядер и электронов она может быть существенно упрощена с помощью адиабатического приближения (приближения Борна-Оппенгеймера). Это приближение строится в два этапа:

1)  положения ядер считаются фиксированными, находится энергия системы, зависящая от координат ядер как от параметров, - ;

2)  движение ядер в потенциале  может рассматриваться как квантово-механически, так и классически.

5.2. Поверхность потенциальной энергии

Рассмотрим подробнее структуру потенциала . Так как трансляция и поворот системы как целого не изменяют суммарной энергии,  зависит реально от 3N-6 координат и может быть представлена в виде поверхности в  3N-5 –мерном пространстве (поверхность потенциальной энергии, ППЭ).

Химическая реакция -  это переход из области ППЭ, соответствующей исходным веществам (“долина исходных веществ”) в область, соответствующую продуктам (“долину продуктов”). Существует множество путей для такого перехода, но среди них есть один, наиболее экономичных с точки зрения энергии. Обозначим длину вдоль этого пути q  и назовем ее координатой реакции. Зависимость энергии от координаты реакции может иметь барьер (точку перевала). Если от точки перевала смещаться перпендикулярно координате реакции, это будет приводить к повышению энергии. Такой барьер называется активационным барьером. Для некоторых реакций (например, для реакции диссоциации молекул на радикалы и пр.) барьер может отсутствовать.

5.3. Модель линии центров

Рассмотрим следующую модель. Будем считать. Что сечение зависит только от относительной поступательной энергии реагентов E_t. Реагирующие молекулы рассматриваются как шары радиуса R_A и R_B . Считается, что реакция протекает только в том случае, если кинетическая энергия, соответствующая компоненте скорости, направленной вдоль линии, соединяющей центры шаров (т.е. перпендикулярной их поверхности) превосходит E₀ (энергию активации). Таким образом, условие протекания реакции таково:

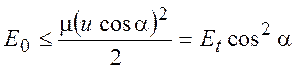                                                                                        (5.1)

Итак, эта модель дает для сечения следующую зависимость от поступательной энергии реагентов:

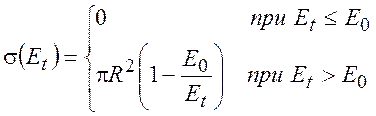                                                                           (5.2)

где

Чтобы найти константу скорости, подставим (5.2) в формулу (1.22). Получим

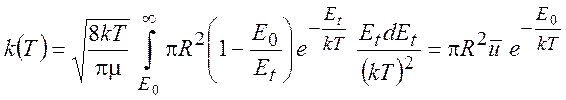                                           (5.3)

где  – средняя относительная скорость молекул:

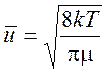
Обозначая

           (фактор двойных столкновений)                                    (5.4)

получим