Основы химической кинетики. Формальная кинетика простых и сложных реакций. Реакции в открытых системах. Механизм элементарного химического превращения, страница 8

Найдем величину . В теории переходного состояния считается, что плотность изображающих точек распределена в фазовом пространстве на поверхности потенциальной энергии (ППЭ) равномерно в соответствии с больцмановским распределением по энергии (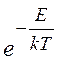). В элементарном объеме фазового пространства системы с s степенями свободы  содержится  состояний (h – постоянная Планка). Следовательно, статистическая сумма системы (полное число возможных состояний) в квазиклассическом приближении равна

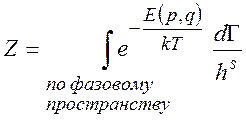                                                                                              (5.12)

Квантовая статистическая сумма системы равна

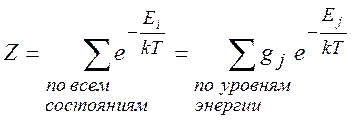                  ( - фактор вырождения)

Тогда величина  выражается через статистические суммы молекулы A  (), молекулы В  () и активированного комплекса  () следующим образом (при этом энергии молекул и активированного комплекса отсчитываются не от одного общего уровня, а от их основного состояния):

                                                                                             (5.13)

В активированном комплексе значение координаты реакции фиксировано на критическом значении . Мы считаем слой  достаточно тонким, так что при смещении внутри слоя в направлении, перпендикулярном критической поверхности, изменением энергии системы можно пренебречь. Тогда состояние системы внутри этого слоя может рассматриваться как одномерное движение активированного комплекса на длине . В этом случае

                                                                                                               (5.14)

где

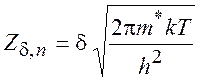   (статистическая сумма поступательного движения)           (5.15)

           - статистическая сумма активированного комплекса.

Окончательно получаем для скорости химической реакции:

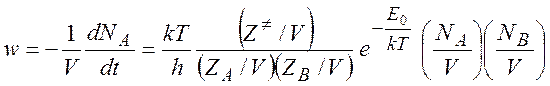                                            (5.16)

и для константы скорости

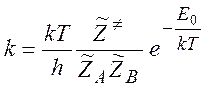                                                                                                   (5.17)

Эта формула является основным результатом метода переходного состояния. Для произвольной элементарной реакции

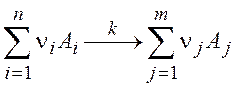
константа скорости выражается через статистические суммы реагентов и активированного комплекса аналогичным образом:

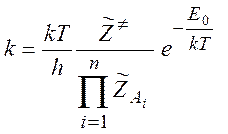                                                                                                 (5.18)

5.6. Статистические суммы

Энергия молекул с неплохой точностью может быть представлена в виде суммы энергий различных движений – электронного, колебательного, вращательного и поступательного. В соответствии с этим статистическая сумма молекулы представляется в виде произведения статистических сумм, относящихся к различным степеням свободы:

                                                                                                (5.19)

Пользуясь выражением (5.12) можно посчитать эти статистические суммы. Приведем здесь результат этих вычислений.

1.  Поступательная статсумма трехмерного движения:

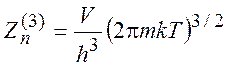                                                                                           (5.20)

2.  Статсумма одномерного вращения вокруг оси:

        ()                                                (5.21)

3.  Вращательная статсумма линейного ротатора:

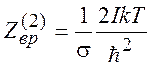                                                                                                        (5.22)

4.  Вращательная статсумма нелинейного ротатора:

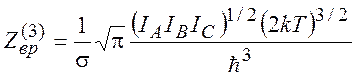                                                                      (5.23)

5.  Колебательная статсумма:

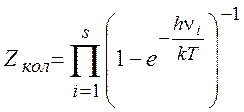                                                                                         (5.24)

6.  Электронная статсумма:

так как обычно электронно-возбужденные состояния молекул лежат очень высоко (по сравнению с kT), то электронные степени свободы полностью заморожены; в этом случае электронная статсумма равна просто степени вырождения основного электронного состояния атома или  молекулы