Обобщенные координаты, принцип возможных перемещений, обобщенные силы

§3.17 Обобщенные координаты, принцип возможных перемещений, обобщенные силы

          Условия, ограничивающие свободу перемещения точек механической системы, называются связями.

            Уравнение связи для одной точки в общем случае имеет вид:

          Будем рассматривать для системы материальных точек связи, в уравнения которых могут входить производные по времени от координат не выше первого порядка:

            Здесь n- число точек системы, l– число связей, наложенных на точки системы.

            Если в уравнения связей входят только координаты и время (), то связь называется геометрической. Если в уравнение входят также и скорости, то связи называются кинематическими. В этом случае уравнения связей являются дифференциальными уравнениями для координат точек. Из геометрических связей дифференцированием можно получить связи кинематические. Из кинематических связей геометрические получаются не всегда, так как дифференциальные уравнения не всегда могут быть проинтегрированы.

            Геометрические и интегрируемые кинематические связи называются голономными. Неинтегрируемые кинематические связи называются неголономными.

            Связи могут быть нестационарными и стационарными, смотря по тому, содержат ли уравнения связей явно время или не содержат.

            Связи бывают неосвобождающими или двухсторонними (уравнения связей выражаются равенствами) и освобождающими или односторонними (уравнения связей выражаются неравенствами).

            Для точки возможным перемещением  называется такое бесконечно малое мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на точку связями. Будем его обозначать .

            Действительным перемещением , которое совершает за время dt, называется такое перемещение, которое точка имеет под действием приложенных сил при заданных начальных условиях и наложенных связях.

            Элементарное действительное перемещение точки принадлежит к числу возможных, если связь стационарна. Возможное перемещение точки  считают изохронной вариацией радиус-вектора, то есть его полным дифференциалом, но при фиксированном времени, когда изменяются (варьируются) только координаты точки.

            Возможным перемещением системы называют любую совокупность возможных перемещений точек системы. Вследствие уравнений связей, наложенных на систему, не все возможные перемещения являются независимыми. Число независимых возможных перемещений называют числом степеней свободы системы.

            Элементарная работа силы на возможном перемещении для точки записывается как

            Для системы материальных точек суммарная элементарная работа сил, приложенных к точкам системы, на возможном перемещении системы имеет вид:

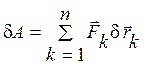, здесь n-число точек системы.

            Обозначим силы реакций связей для точек системы через . Тогда связи называются идеальными, если для любого возможного перемещения системы выполняется условие

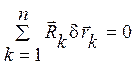
            К идеальным, в частности, относятся все связи без трения, связи точек в абсолютно твердом теле, гибкие нерастяжимые нити, канаты и тросы, а также закрепленные точки системы.

            С помощью сделанных определений сформулируем теперь принцип возможных перемещений, который, если принять его за аксиому, может быть основой построения всех положений статики.

            Для равновесия механической системы, подчиненной идеальным, стационарным и неосвобождающим связям, необходимо и достаточно, чтобы сумма элементарных работ всех активных сил, приложенных к точкам системы, была равной нулю при любом возможном перемещении системы, если скорости точек системы в рассматриваемый момент времени равны нулю, то есть

.

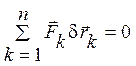            Обобщенные координаты – это независимые параметры, однозначно определяющие положение системы в пространстве.

;

            Здесь m-число степеней свободы системы, то есть число независимых обобщенных координат, однозначно определяющих положение системы.

            Используя уравнения связей  (здесь l-число связей, наложенных на систему) и выражения обобщенных координат через декартовы при разрешимости этой системы уравнений можно выразить декартовы координаты через обобщенные:

            Для стационарных связей время явно не входит в уравнения связей, поэтому оно и в  войдет только неявно.

            Найдем вариацию радиус-векторов  и составим выражение для работы внешних сил, действующих на точки системы:

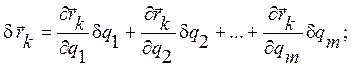
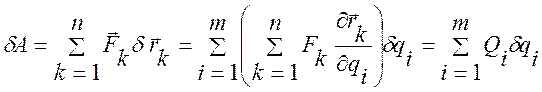     (3.17.1)

            Выражение в круглых скобках, стоящее сомножителем перед dq_i, называется обобщенной силой Q_i, соответствующей обобщенной координате q_i.

            Тогда принцип возможных перемещений в обобщенных координатах будет выглядеть следующим образом:

            А поскольку все обобщенные координаты независимы, то это может быть только тогда, когда

            Последнее выражение есть следствие, означающее: система находится в равновесии тогда и только тогда, когда все ее обобщенные силы равны нулю.

            Для вычисления обобщенных сил механической системы обычно используется один из двух методов: